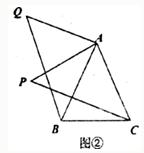
26、复习“全等三角形”的知识时，老师布置了一道作业题：“如下图①，已知在△ABC中，AB=AC，P是△ABC内部任意一点，将AP绕A顺时针旋转至AQ，使得∠QAP=∠BAC，连接BQ、CP，则BQ=CP．”
（1）小亮是个爱动脑筋的同学，他通过对图①的分析，证明了△ABQ≌△ACP，从而证得BQ=CP．请你帮小亮完成证明．
（2）之后，小亮又将点P移到等腰三角形ABC之外，原题中的条件不变，“BQ=CP”仍然成立吗？若成立，请你就图②给出证明．若不成立，请说明理由．

查看答案和解析>>

复习“全等三角形”的知识时，老师布置了一道作业题：“如下图①，已知在△ABC中，AB=AC，P是△ABC内部任意一点，将AP绕A顺时针旋转至AQ，使得∠QAP=∠BAC，连接BQ、CP，则BQ=CP．”
（1）小亮是个爱动脑筋的同学，他通过对图①的分析，证明了△ABQ≌△ACP，从而证得BQ=CP．请你帮小亮完成证明．
（2）之后，小亮又将点P移到等腰三角形ABC之外，原题中的条件不变，“BQ=CP”仍然成立吗？若成立，请你就图②给出证明．若不成立，请说明理由．

查看答案和解析>>

复习“全等三角形”的知识时，老师布置了一道作业题：“如下图①，已知在△ABC中，AB=AC，P是△ABC内部任意一点，将AP绕A顺时针旋转至AQ，使得∠QAP=∠BAC，连接BQ、CP，则BQ=CP．”
（1）小亮是个爱动脑筋的同学，他通过对图①的分析，证明了△ABQ≌△ACP，从而证得BQ=CP．请你帮小亮完成证明．
（2）之后，小亮又将点P移到等腰三角形ABC之外，原题中的条件不变，“BQ=CP”仍然成立吗？若成立，请你就图②给出证明．若不成立，请说明理由．

查看答案和解析>>

复习“全等三角形”的知识时，老师布置了一道作业题：“如图①，已知，在△ABC中，AB＝AC，P是△ABC中内任意一点，将AP绕点A顺时针旋转至AQ，使∠QAP＝∠BAC，连结BQ、CP则BQ＝CP．”

小亮是个爱动脑筋的同学，他通过对图①的分析，证明了△ABC≌△ACP，从而证得BQ＝CP．之后，他将点P移到等腰三角形ABC外，原题中其它条件不变，发现“BQ＝CP”仍然成立，请你就图②给出证明．

查看答案和解析>>

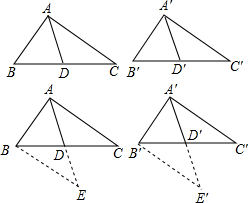（2013•莒南县一模）【典型练习】如果两个三角形有两条边和其中一边上的中线对应相等，那么这两个三角形全等．（无需证明）
【拓展变式】小明很顺利的完成了上面的练习后，又进一步对该命题进行了发散思维，把原命题中的一些条件进行了变换，得到了如下三个不同的命题：
（1）如果两个三角形有两条边和第三边上的中线对应相等，那么这两个三角形全等．
（2）如果两个三角形有两条边和第三边上的高对应相等，那么这两个三角形全等．
（3）如果两个三角形有两条边和夹角的平分线对应相等，那么这两个三角形全等．
【探索新知】小明对这三个命题，无法判断其命题的真假，于是他向老师求教．数学老师对命题（1）做出了一些指导，请你帮助小明完成下面的解答过程．
已知：如图，AB=A′B′，AD=A′D′，AD是BC边上的中线，A′D′是B′C′边上的中线，求证：△ABC≌△A′B′C′，
证明：如图，延长AD至E使AD=DE，连接BE，延长A′D′至E′使A′D′=D′E′，连接B′E′．
【合作学习】对于命题（2）、（3），你能帮助小明判断命题的真假吗？如果是真命题，请给完整的证明，如果是假命题，在下面的空白处做出解答．（要求：画出图形，说明理由．）

查看答案和解析>>

一、选择题

1．Ｂ   2．A    3．B    4．C    5．Ｃ    6．D    7．A    8．B

二、填空题

9． 115°     10．  （x+1） （x-1）    11． x＞3     12．  1.57×10¹⁰

13．  105     14．       15．  8和2        16．199

三、解答题

17．计算

解： 原式=1+5（后面三个数中每计算正确一个得2分）     ???????????????????????????? 2分

= 115                                                                             ???????????????????????????? 4分

= 5                                                                                ???????????????????????????? 6分

18．解： ??????????????? 2分

    ，???????????????????????????????????????????????????????????????????????????????? 3分

解法一：，． 均为正数，

    只取．????????????????????????????????????????????????????????????????? 5分

    原式．????????????????????????? 6分

解法二：，且均为正数，

（负值舍去）， ．????????????????????????????????????????????????????????????????????????????????? 5分

  以下同解法一  也可以，原式．???????????????? 6分

19．解：设接待1日游旅客人，接待3日游旅客，根据题意得??????????????????????????????? 1分

                                                                                           3分

解这个方程组，得                                                                                       5分

答：该旅行社接待1日游旅客600人，接待3日游旅客1000人．?????????????????????????????????? 6分

20．解： （1）  A（，3），B（，1），C（，0）             ???????????????????????????? 3分

（2）图略????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 6分

（3）???????????????????????????????????????????????????????????????????????????????????????????????????????????? 8分

21．所添加条件为PA=PB???????????????????????????????????????????????????????????????????????????????????????????? 2分

得到的一对全等三角形是△PAD≌△PBC  ??????????????????????????????????????????????????????????????????? 4分

证明：∵PA=PB ??????????????????????????????????????????????????????????????????????????????????????????????????????????? 5分

∴∠A=∠B  ????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 6分

又∵AD=BC   ?????????????????????????????????????????????????????????????????????????????????????????????????????????????? 7分

∴△PAD≌△PBC ???????????????????????????????????????????????????????????????????????????????????????????????????????? 8分

所添加条件，只要能证明三角形全等，按上面评分标准给分．

22．解：  （1） 50 ?????????????????????????????????????????????????????????????????????????????????????????????????? 2分

（2）设函数的解析式为y =kx+b，由题意得

  解方程组得   ????????????????????????????????????????????????????????????????? 3分

所以函数的解析式为y =x70    ????????????????????????????????????????????????????????????????????????????????? 4分

（3） 解不等式x70＞120得x＞190   

因此，至少要售出190份早餐，才能使每天有120元以上的盈利．???????????????????????????????? 6分

（4）该店每出售一份早餐，盈利1元．     ??????????????????????????????????????????????????????????????? 8分

23．解：（1）解方程得?????????????????????????????????????????????????? 1分

列表：

2

3

4

1

1，2

1，3

1，4

2

2，2

2，3

2，4

3

3，2

3，3

3，4

 （或用树状图）??????????????????????????????????????????????????????????????????????????????????????????????????????????? 2分

由表知：指针所指两数都是该方程解的概率是：???????????????????????????????????????????????????????? 3分

指针所指两数都不是该方程解的概率是：?????????????????????????????????????????????????????????????????? 4分

（2）不公平！??????????????????????????????????????????????????????????????????????????????????????? 5分

修改得分规则为：

指针所指两个数字都是该方程解时，王磊得1分．???????????????????????????????????????????????????????? 6分

指针所指两个数字都不是该方程解时，张浩得4分．????????????????????????????????????????????????????? 7分

此时?????????????????????????????????????????????????????????????????????????????????????????????????????????? 8分

⌒ ⌒ ∵AB=BD  ∴ A B=B D   ∴∠BDE =∠BCD???????????????????????????????????????????????????????????????? 3分 又∵∠DBE =∠DBC       ∴△BDE∽△BCD     ∴???????????????????????????????? 4分 ⌒ ⌒ ⌒ ⌒ ⌒ ⌒ （3）在（1）和（2）的条件下，．∵A B=B D=D C    ∴∠BDA =∠DAC   ∴ BD∥OA 又∵AB∥DO         ∴四边形AODB是平行四边形     ??????????????????????????????????????????? 9分 ∵OA=OD        　  ∴平行四边形AODB是菱形  ????????????????????????????????????????????????? 10分   25．解：（1）点 M   ????????????????????????????????????????????????????????????????????????????????????????????????? 1分 （2）经过t秒时，， 则， ∵== ∴    ∴   ????????????????????????????????????????????????????????????????? 2分 ∴   ?????????????????????????????????????????????????????????????????????????????????????????????????????????????? 3分 ∴  ????????????????????????????????????????????????????????????????????????????? 5分 ∵∴当时，S的值最大．   ????????????????????????????????????????????????????????????????? 6分 （3）存在．     ????????????????????????????????????????????????????????????????????????????????????????????????????????? 7分 设经过t秒时，NB=t，OM=2t 则， ∴==         ??????????????????????????????????????????????????????????????????????????????? 8分 ①若，则是等腰Rt△底边上的高 ∴是底边的中线     ∴ ∴ ∴ ∴点的坐标为（1，0）     ?????????????????????????????????????????????????????????????????????????????????? 10分 ②若，此时与重合 ∴ ∴ ∴ ∴点的坐标为（2，0）     ?????????????????????????????????????????????????????????????????????????????????? 12分   同步练习册答案 全品作业本答案 同步测控优化设计答案 长江作业本同步练习册答案 同步导学案课时练答案 仁爱英语同步练习册答案 一课一练创新练习答案 时代新课程答案 新编基础训练答案 能力培养与测试答案 更多练习册答案 国际学校优选 - 练习册列表 - 试题列表 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com 版权声明：本站所有文章，图片来源于网络，著作权及版权归原作者所有，转载无意侵犯版权，如有侵权，请作者速来函告知，我们将尽快处理，联系qq：3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号