题目列表(包括答案和解析)
设函数f(x)的定义域为R，
，且F(1，y)＝
y2－y＋5
(1)求证：f(y－1)＝y2－2y＋10
(2)求F(x，y)的表达式．
(3)定义xn+1＝F(xn，0)，且x1＝6，证明数列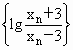
是等比数列，并求其前n项的和sn
记Sn为数列{an}的前n项和，给出两个数列：
①5，3，1，－1，－3，－5，－7，……
②―14，―10，―6，―2，2，6，10，14，18，……
(1)对于数列①，计算S1，S2，S4，S5；对于数列②，计算S1，S3，S5，S7；
(2)根据上述结果，对于存在正整数k，满足ak＋ak+1＝0的等差数列{an}，求证：Sn＝S2k－n．
当n为正整数时，函数N(n)表示n的最大奇因数，如N(3)＝3，N(10)＝5，…，设Sn＝n(1)＋N(2)＋N(3)＋N(4)＋…＋N(2n－1)＋N(2n)，则Sn＝________．
已知公比为q(0＜q＜1)的无穷等比数列{an}各项的和为9，无穷等比数列{a
}各项的和为
．
(Ⅰ)求数列{an}的首项a1和公比q；
(Ⅱ)对给定的k(k＝1，2，3，…，n)，设T(k)是首项为ak，公差为2ak－1的等差数列，求T(2)的前10项之和；
(Ⅲ)设bi为数列T(k)的第i项，Sn＝b1＋b2＋…＋bn，求Sn，并求正整数m(m＞1)，使得
存在且不等于零．(注：无穷等比数列各项的和即当n→∞时该无穷等比数列前n项和的极限)
等比数列{an}中，a1，a2，a3分别是下表第一、二、三行中的某一个数，且a1，a2，a3中的任何两个数不在下表的同一列.
|
| 第一列 | 第二列 | 第三列 |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 6 | 4 | 14 |
| 第三行 | 9 | 8 | 18 |
(1)求数列{an}的通项公式；
(2)若数列{bn}满足：bn＝an＋(－1)nln an，求数列{bn}的前n项和Sn.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com