
题目列表(包括答案和解析)
函数![]() 的最小正周期为
的最小正周期为![]() ,且其图像向右平移
,且其图像向右平移![]() 个单位后得到的函数为奇函数,则函数
个单位后得到的函数为奇函数,则函数
![]() 的图象
的图象
A.关于点![]() 对称 B.关于直线
对称 B.关于直线![]() 对称
对称
函数f(x)=sin(wx+j)(|j|<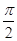 )的最小正周期为p,且其图像向右平移
)的最小正周期为p,且其图像向右平移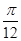 个单位后得到的函数为奇函数,则函数f(x)的图象(
)
个单位后得到的函数为奇函数,则函数f(x)的图象(
)
A.关于点(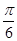 ,0)对称
B.关于直线x=
,0)对称
B.关于直线x=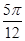 对称
对称
C.关于点(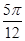 ,0)对称
D.关于直线x=
,0)对称
D.关于直线x=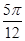 对称
对称
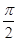 )的最小正周期为p,且其图像向右平移
)的最小正周期为p,且其图像向右平移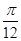 个单位后得到的函数为奇函数,则函数f(x)的图象( )
个单位后得到的函数为奇函数,则函数f(x)的图象( )A.关于点(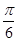 ,0)对称 ,0)对称 | B.关于直线x=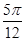 对称 对称 |
C.关于点(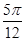 ,0)对称 ,0)对称 | D.关于直线x=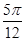 对称 对称 |
给出下列命题:
① 存在实数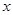 使得
使得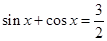 ②若
②若 为第一象限角且
为第一象限角且 ,则
,则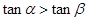 ③函数
③函数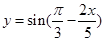 的最小正周期为
的最小正周期为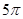 ,④ 函数
,④ 函数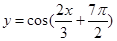 是奇函数 ⑤函数
是奇函数 ⑤函数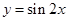 的图像向左平移
的图像向左平移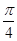 个单位,得到
个单位,得到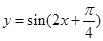 的图像。其中正确命题的序号是
(把你认为正确的序号都填上)
的图像。其中正确命题的序号是
(把你认为正确的序号都填上)
给出下列命题:
① 存在实数![]() 使得
使得![]() ②若
②若![]() 为第一象限角且
为第一象限角且![]() ,则
,则![]() ③函数
③函数![]() 的最小正周期为
的最小正周期为![]() ,④ 函数
,④ 函数![]() 是奇函数 ⑤函数
是奇函数 ⑤函数![]() 的图像向左平移
的图像向左平移![]() 个单位,得到
个单位,得到![]() 的图像。其中正确命题的序号是 (把你认为正确的序号都填上)
的图像。其中正确命题的序号是 (把你认为正确的序号都填上)
一、选择题:
|