
题目列表(包括答案和解析)
解:能否投中,那得看抛物线与篮圈所在直线是否有交点。因为函数![]() 的零点是-2与4,篮圈所在直线x=5在4的右边,抛物线又是开口向下的,所以投不中。
的零点是-2与4,篮圈所在直线x=5在4的右边,抛物线又是开口向下的,所以投不中。
某城市出租汽车的起步价为10元,行驶路程不超出4km,则按10元的标准收租车费![]() 若行驶路程超出4km,则按每超出lkm加收2元计费(超出不足1km的部分按lkm计).从这个城市的民航机场到某宾馆的路程为15km.某司机常驾车在机场与此宾馆之间接送旅客,由于行车路线的不同以及途中停车时间要转换成行车路程(这个城市规定,每停车5分钟按lkm路程计费),这个司机一次接送旅客的行车路程ξ是一个随机变量,
若行驶路程超出4km,则按每超出lkm加收2元计费(超出不足1km的部分按lkm计).从这个城市的民航机场到某宾馆的路程为15km.某司机常驾车在机场与此宾馆之间接送旅客,由于行车路线的不同以及途中停车时间要转换成行车路程(这个城市规定,每停车5分钟按lkm路程计费),这个司机一次接送旅客的行车路程ξ是一个随机变量,
(1)他收旅客的租车费η是否也是一个随机变量?如果是,找出租车费η与行车路程ξ的关系式;
(2)已知某旅客实付租车费38元,而出租汽车实际行驶了15km,问出租车在途中因故停车累计最多几分钟?这种情况下,停车累计时间是否也是一个随机变量?
(本小题满分12分)函数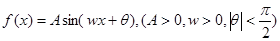 的一系列对应值如下表:
的一系列对应值如下表:
|
|
…… |
|
0 |
|
|
|
|
|
…. |
|
|
….. |
0 |
1 |
|
0 |
—1 |
|
0 |
….. |
(1)根据表中数据求出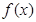 的解析式;
的解析式;
(2)指出函数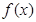 的图象是由函数
的图象是由函数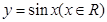 的图象经过怎样的变化而得到的;
的图象经过怎样的变化而得到的;
(3)令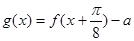 ,若
,若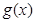 在
在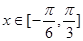 时有两个零点,求
时有两个零点,求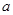 的取值范围。
的取值范围。
(本小题满分12分)函数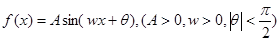 的一系列对应值如下表:
的一系列对应值如下表:
|
|
。。。 |
|
0 |
|
|
|
|
|
。。。 |
|
|
。。。 |
0 |
1 |
|
0 |
—1 |
|
0 |
。。。 |
(1)根据表中数据求出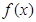 的解析式;
的解析式;
(2)指出函数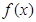 的图象是由函数
的图象是由函数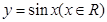 的图象经过怎样的变化而得到的;
的图象经过怎样的变化而得到的;
(3)令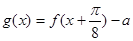 ,若
,若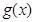 在
在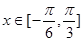 时有两个零点,求
时有两个零点,求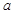 的取值范围。
的取值范围。
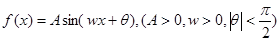 的一系列对应值如下表:
的一系列对应值如下表: | 。。。 |  | 0 |  |  |  |  |  | 。。。 |
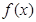 | 。。。 | 0 | 1 |  | 0 | —1 |  | 0 | 。。。 |
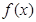 的解析式;
的解析式;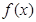 的图象是由函数
的图象是由函数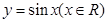 的图象经过怎样的变化而得到的;
的图象经过怎样的变化而得到的;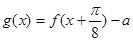 ,若
,若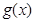 在
在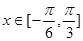 时有两个零点,求
时有两个零点,求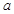 的取值范围。
的取值范围。设椭圆  :
: (
( )的一个顶点为
)的一个顶点为 ,
, ,
, 分别是椭圆的左、右焦点,离心率
分别是椭圆的左、右焦点,离心率
 ,过椭圆右焦点
,过椭圆右焦点
 的直线
的直线  与椭圆
与椭圆  交于
交于 ,
, 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2)是否存在直线  ,使得
,使得
 ,若存在,求出直线
,若存在,求出直线
 的方程;若不存在,说明理由;
的方程;若不存在,说明理由;
【解析】本试题主要考查了椭圆的方程的求解,以及直线与椭圆的位置关系的运用。(1)中椭圆的顶点为 ,即
,即 又因为
又因为 ,得到
,得到 ,然后求解得到椭圆方程(2)中,对直线分为两种情况讨论,当直线斜率存在时,当直线斜率不存在时,联立方程组,结合
,然后求解得到椭圆方程(2)中,对直线分为两种情况讨论,当直线斜率存在时,当直线斜率不存在时,联立方程组,结合 得到结论。
得到结论。
解:(1)椭圆的顶点为 ,即
,即
 ,解得
,解得 ,
,
 椭圆的标准方程为
椭圆的标准方程为 --------4分
--------4分
(2)由题可知,直线 与椭圆必相交.
与椭圆必相交.
①当直线斜率不存在时,经检验不合题意. --------5分
②当直线斜率存在时,设存在直线 为
为 ,且
,且 ,
, .
.
由 得
得 , ----------7分
, ----------7分
 ,
, ,
,

=
所以 ,
----------10分
,
----------10分
故直线 的方程为
的方程为 或
或
即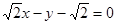 或
或
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com