
题目列表(包括答案和解析)
定义在 上的函数
上的函数 对任意
对任意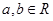 都有
都有 (
(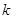 为常数).
为常数).
(1)判断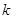 为何值时
为何值时 为奇函数,并证明;
为奇函数,并证明;
(2)设 ,
, 是
是 上的增函数,且
上的增函数,且 ,若不等式
,若不等式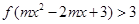 对任意
对任意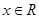 恒成立,求实数
恒成立,求实数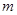 的取值范围.
的取值范围.
定义在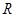 上的函数
上的函数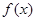 对任意
对任意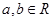 都有
都有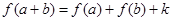 (
(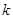 为常数).
为常数).
(1)判断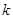 为何值时
为何值时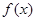 为奇函数,并证明;
为奇函数,并证明;
(2)设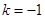 ,
,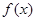 是
是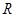 上的增函数,且
上的增函数,且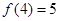 ,若不等式
,若不等式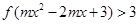 对任意
对任意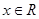 恒成立,求实数
恒成立,求实数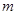 的取值范围.
的取值范围.
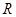 上的函数
上的函数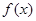 对任意
对任意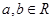 都有
都有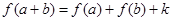 (
(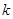 为常数).
为常数).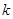 为何值时
为何值时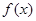 为奇函数,并证明;
为奇函数,并证明;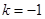 ,
,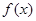 是
是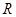 上的增函数,且
上的增函数,且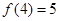 ,若不等式
,若不等式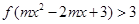 对任意
对任意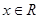 恒成立,求实数
恒成立,求实数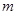 的取值范围.
的取值范围.已知方程tan2x一 tan
x+1=0在x
tan
x+1=0在x [0,n
[0,n )( n
)( n N*)内所有根的和记为an
N*)内所有根的和记为an
(1)写出an的表达式;(不要求严格的证明)
(2)记Sn = a1 + a2 +…+ an求Sn;
(3)设bn =(kn一5)  ,若对任何n
,若对任何n N* 都有an
N* 都有an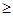 bn,求实数k的取值范围.
bn,求实数k的取值范围.
已知方程tan2x一 tan x+1=0在x
tan x+1=0在x [0,n
[0,n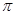 )( n
)( n N*)内所有根的和记为an
N*)内所有根的和记为an
(1)写出an的表达式;(不要求严格的证明)
(2)记Sn = a1 + a2 +…+ an求Sn;
(3)设bn =(kn一5) 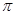 ,若对任何n
,若对任何n N* 都有an
N* 都有an bn,求实数k的取值范围.
bn,求实数k的取值范围.
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
A
C
D
C
C
B
C
B
B
D
二、填空题
11.100 12.4 13.(-2,2) 14.
15. 16.
16. 17.
17.
18.(本小题14分)
解答:(1)设甲选手答对一个问题的正确率为 ,则
,则
故甲选手答对一个问题的正确率 3分
3分
(Ⅱ)选手甲答了3道题目进入决赛的概率为 =
= 4分
4分
选手甲答了4道题目进入决赛的概率为 5分
5分
选手甲答了5道题目进入决赛的概率为 6分
6分
选手甲可以进入决赛的概率 8分
8分
(Ⅲ) 可取3,4,5
可取3,4,5
则有 9分
9分
 10分
10分
 11分
11分
因此有 (直接列表也给分)

3
4
5




故 14分
14分
19.解:由三视图知,该多面体是低面为直角三角形的直三棱柱


(1)证明:连续取 ,易见
,易见 通过点
通过点 ,连接
,连接 。
。
 4分
4分
(2)作 于
于 ,连接
,连接
面


 故
故 为所求二面角的平面角。 6分
为所求二面角的平面角。 6分
在 中
中
故所求二面角的余弦值为 9分
9分
(3)棱锥 的体积
的体积 14分
14分
20 解:(1)解方程得 或
或 1分
1分
 当
当 时,
时, 或
或 ,此时
,此时 2分
2分
当 时,
时, 3分
3分
依次类推:
 5分
5分
(2)

 9分
9分
(3)由 得
得


 11分
11分
设
易证 在
在 上单调递减,在(
上单调递减,在( )上单调递增。 13分
)上单调递增。 13分



 15分
15分
21.解:(1)设 由
由 得
得
直线 的方程为:
的方程为:
直线 的方程为:
的方程为:
解方程组得 3分
3分
 由已知,
由已知, 三点共线,设直线
三点共线,设直线 的方程为:
的方程为:
与抛物线方程 联立消
联立消 可得:
可得:
 5分
5分
所以 点的纵坐标为-2,所以线段
点的纵坐标为-2,所以线段 中点的纵坐标O
中点的纵坐标O
即线段 被
被 轴平分。
6分
轴平分。
6分
(2)


=0 9分



 13分
13分
 而
而  所以在直角
所以在直角 中,
中,
由影射定理即得 15分
15分
22.解:(1) 代入得
代入得
设 1分
1分

 3分
3分
令 解得
解得
 在
在 上单调递减,在
上单调递减,在 上单调递增。 5分
上单调递增。 5分
 即原式的最小值为-1
7分
即原式的最小值为-1
7分
(2)要证 即证
即证
即证
即证 9分
9分
由已知 设
设 10分
10分
 11分
11分


 13分
13分
所以 在
在 上单调递减,
上单调递减, 
原不等式得证。 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com