
题目列表(包括答案和解析)
(本题满分18分,第(1)小题4分,第2小题6分,第3小题8分)
已知点,![]() ,…,
,…,![]() (
(![]() 为正整数)都在函数
为正整数)都在函数![]() 的图像上,其中
的图像上,其中![]() 是以1为首项,2为公差的等差数列。
是以1为首项,2为公差的等差数列。
(1)求数列![]() 的通项公式,并证明数列
的通项公式,并证明数列![]() 是等比数列;
是等比数列;
(2)设数列![]() 的前
的前![]() 项的和
项的和![]() ,求
,求![]() ;
;
(3)设![]() ,当
,当![]() 时,问
时,问![]() 的面积是否存在最大值?若存在,求出最大值;若不存在,请说明理由;
的面积是否存在最大值?若存在,求出最大值;若不存在,请说明理由;
(本题满分18分,第(1)小题4分,第2小题6分,第3小题8分)
已知函数![]() ,实数
,实数![]() 且
且![]() 。
。
(1)设![]() ,判断函数
,判断函数![]() 在
在![]() 上的单调性,并说明理由;
上的单调性,并说明理由;
(2)设![]() 且
且![]() f(x)的定义域和值域都是
f(x)的定义域和值域都是![]() ,求
,求![]() 的最大值;
的最大值;
(3) 若不等式![]() 对
对![]() 恒成立,求
恒成立,求![]() 的范围;
的范围;
(本大题满分18分)本大题共有3个小题,第1小题满分4分,第2小题满6分,第3小题满8分.
已知函数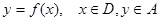 ;
;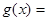
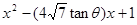 ,
,
(1)当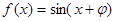 为偶函数时,求
为偶函数时,求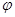 的值。
的值。
(2)当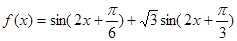 时,
时,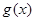 在
在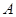 上是单调递增函数,求
上是单调递增函数,求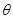 的取值范围。
的取值范围。
(3)当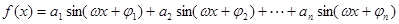 时,(其中
时,(其中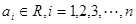 ,
,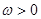 ),若
),若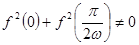 ,且函数
,且函数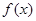 的图像关于点
的图像关于点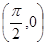 对称,在
对称,在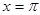 处取得最小值,试探讨
处取得最小值,试探讨 应该满足的条件。
应该满足的条件。
 ;
;
 ,
, 为偶函数时,求
为偶函数时,求 的值。
的值。 时,
时, 在
在 上是单调递增函数,求
上是单调递增函数,求 的取值范围。
的取值范围。 时,(其中
时,(其中 ,
, ),若
),若 ,且函数
,且函数 的图像关于点
的图像关于点 对称,在
对称,在 处取得最小值,试探讨
处取得最小值,试探讨 应该满足的条件。
应该满足的条件。某港口的水深 (米)是时间
(米)是时间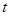 (
( ,单位:小时)的函数,下面是每天时间与水深的关系表:
,单位:小时)的函数,下面是每天时间与水深的关系表:
|
|
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
|
10 |
13 |
9.9 |
7 |
10 |
13 |
10.1 |
7 |
10 |
经过长期观测,  可近似的看成是函数
可近似的看成是函数 ,(本小题满分14分)
,(本小题满分14分)
(1)根据以上数据,求出 的解析式。
的解析式。
(2)若船舶航行时,水深至少要11.5米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
【解析】第一问由表中数据可以看到:水深最大值为13,最小值为7,,
∴A+b=13, -A+b=7 解得 A=3, b=10
第二问要想船舶安全,必须深度 ,即
,即
∴

解得:
 得到结论。
得到结论。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com