
题目列表(包括答案和解析)
设向量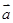 与
与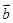 的夹角为
的夹角为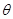 ,定义
,定义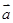 与
与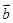 的“向量积”:
的“向量积”: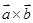 是一个向量,它的模
是一个向量,它的模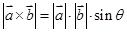 ,若
,若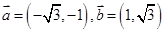 ,则
,则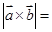 ( )
( )
A.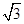 B.2 C.
B.2 C.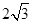 D.4
D.4
设向量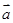 与
与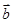 的夹角为
的夹角为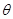 ,定义
,定义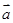 与
与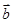 的“向量积”:
的“向量积”: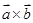 是一个向量,它的模
是一个向量,它的模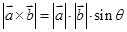 ,若
,若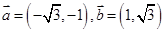 ,则
,则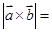 ( )
( )
A.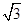 B.2 C.
B.2 C. 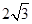 D.4
D.4
.设向量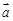 与
与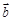 的夹角为
的夹角为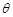 ,定义
,定义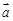 与
与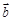 的“向量积”:
的“向量积”: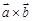 是一个向量,它的模
是一个向量,它的模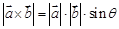 ,若
,若 ,则
,则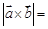 ( )
( )
A.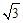 B.2 C.
B.2 C.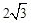 D.4
D.4
设向量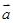 与
与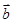 的夹角为
的夹角为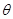 ,定义
,定义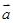 与
与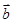 的“向量积”:
的“向量积”: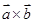 是一个向量,它的模
是一个向量,它的模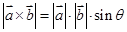 ,若
,若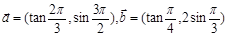 ,则
,则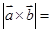 ( )
( )
A.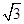 B. 2
C.
B. 2
C. 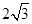 D.4
D.4
设向量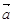 与
与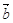 的夹角为
的夹角为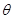 ,定义
,定义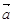 与
与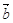 的“向量积”:
的“向量积”: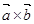 是一个向量,它的模为
是一个向量,它的模为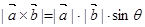 .若
.若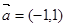 ,
,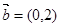 ,则
,则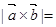 _____________.
_____________.
一、选择题 1--5 ADACB 6--10 ABACD 11―12 CB
二、填空题 13.8 14.7 15.12 16.AB
三、解答题
17.解:(Ⅰ) 卷.files/image278.gif) ,
,
卷.files/image280.gif) ,
,
卷.files/image282.gif) .…………………………(4分)
.…………………………(4分)
卷.files/image284.gif)
卷.files/image286.gif) ,
, 卷.files/image288.gif) .………………………(6分)
.………………………(6分)
(Ⅱ)由余弦定理卷.files/image290.gif) ,得
,得 卷.files/image292.gif) .………(8分)
.………(8分)
卷.files/image294.gif) ,
, 卷.files/image296.gif) .
.
卷.files/image147.jpg)
卷.files/image147.jpg) 所以
所以卷.files/image298.gif) 的最小值为
的最小值为卷.files/image300.gif) ,当且仅当
,当且仅当卷.files/image302.gif) 时取等号.………………(12分)
时取等号.………………(12分)
卷.files/image147.jpg) 18.(Ⅰ)解法一:依据题意,因为队伍从水路或陆路抵达灾区的概率相等,则将“队伍从水路或陆路抵达灾区”视为同一个事件. 记“队伍从水路或陆路抵达灾区”为事件C,且B、C相互独立,而且
18.(Ⅰ)解法一:依据题意,因为队伍从水路或陆路抵达灾区的概率相等,则将“队伍从水路或陆路抵达灾区”视为同一个事件. 记“队伍从水路或陆路抵达灾区”为事件C,且B、C相互独立,而且卷.files/image304.gif) .……………………………(2分)
.……………………………(2分)
在5月13日恰有1支队伍抵达灾区的概率是
卷.files/image306.gif) .……………………(6分)
.……………………(6分)
解法二:在5月13日恰有1支队伍抵达灾区的概率是
卷.files/image308.gif) .…………(6分)
.…………(6分)
(Ⅱ)依据题意,因为队伍从水路或陆路抵达灾区的概率相等,则将“队伍从水路或陆路抵达灾区”视为同一个事件. 记“队伍从水路或陆路抵达灾区”为事件C,且B、C相互独立,而且卷.files/image304.gif) .
.
设5月13日抵达灾区的队伍数为卷.files/image311.gif) ,则
,则卷.files/image313.gif) =0、1、2、3、4. ……………………(7分)
=0、1、2、3、4. ……………………(7分)
由已知有:卷.files/image315.gif) ;
;
卷.files/image317.gif) ;
;
卷.files/image319.gif) ;
;
卷.files/image321.gif) ;
;
卷.files/image323.gif) .
.
答:在5月13日抵达灾区的队伍数为2时概率最大……………………(12分)
19. (I)由已知a2-a1=-2, a3-a2=-1, -1-(-2)=1
∴an+1-an=(a2-a1)+(n-1)?1=n-3
n≥2时,an=( an-an-1)+( an-1-an-2)+…+( a3-a2)+( a2-a1)+ a1
=(n-4)+(n-5) +…+(-1)+(-2)+6 =卷.files/image325.gif)
n=1也合适. ∴an=卷.files/image325.gif) (n∈N*) ……………………3分
(n∈N*) ……………………3分
又b1-2=4、b2-2=2 .而卷.files/image327.gif) ∴bn-2=(b1-2)?(
∴bn-2=(b1-2)?(卷.files/image329.gif) )n-1即bn=2+8?(
)n-1即bn=2+8?(卷.files/image329.gif) )n……(6分)
)n……(6分)
∴数列{an}、{bn}的通项公式为:an=卷.files/image325.gif) ,bn=2+(
,bn=2+(卷.files/image329.gif) )n-3
)n-3
卷.files/image147.jpg) (II)设
(II)设卷.files/image331.gif)
卷.files/image147.jpg)
卷.files/image147.jpg) 当k≥4时
当k≥4时卷.files/image333.gif) 为k的增函数,-8?(
为k的增函数,-8?(卷.files/image329.gif) )k也为k的增函数,而f(4)=
)k也为k的增函数,而f(4)= 卷.files/image329.gif)
卷.files/image147.jpg) ∴当k≥4时ak-bk≥
∴当k≥4时ak-bk≥卷.files/image329.gif) ………………10分
………………10分
又f(1)=f(2)=f(3)=0 ∴不存在k, 使f(k)∈(0,卷.files/image329.gif) )…………12分
)…………12分
20解法1:(Ⅰ)因为M是底面BC边上的中点,且AB=AC,所以AM卷.files/image335.gif) BC,
BC,
卷.files/image336.gif) 在正三棱柱ABC-A1B1C1中,
在正三棱柱ABC-A1B1C1中,卷.files/image338.gif) 底面
底面卷.files/image340.gif) ,
, 卷.files/image342.gif) AM
AM卷.files/image335.gif)
卷.files/image344.gif) 又
又卷.files/image346.gif) .所以AM
.所以AM卷.files/image335.gif) 平面
平面卷.files/image348.gif)
卷.files/image350.gif) .
.
(或:连结卷.files/image352.gif) ,
,卷.files/image354.gif) 又
又卷.files/image356.gif) ,
,卷.files/image358.gif) .)…………(5分)
.)…………(5分)
(II)因为AM卷.files/image335.gif) 平面
平面卷.files/image348.gif)
卷.files/image350.gif)
且卷.files/image350.gif) M
M卷.files/image360.gif) 平面
平面卷.files/image348.gif)
卷.files/image350.gif) ,NM
,NM卷.files/image360.gif) 平面
平面卷.files/image348.gif)
卷.files/image350.gif)
∴AM卷.files/image335.gif)
卷.files/image350.gif) M, AM
M, AM卷.files/image335.gif) NM,
NM,
∴卷.files/image362.gif)
卷.files/image350.gif) MN为二面角
MN为二面角卷.files/image350.gif) ―AM―N的平面角. …………(7分)
―AM―N的平面角. …………(7分)
∴卷.files/image364.gif) ,设C1N=
,设C1N=卷.files/image366.gif) ,则CN=1-
,则CN=1-卷.files/image366.gif)
又卷.files/image350.gif) M=
M=卷.files/image368.gif)
卷.files/image370.gif) ,MN=
,MN=卷.files/image372.gif) ,
,
卷.files/image374.jpg) 连
连卷.files/image350.gif) N,得
N,得卷.files/image350.gif) N=
N=卷.files/image376.gif) ,
,
在卷.files/image378.gif)
卷.files/image350.gif) MN中,由余弦定理得
MN中,由余弦定理得
卷.files/image380.gif) , …(10分)
, …(10分)
得卷.files/image366.gif) =
=卷.files/image382.gif) .故
.故卷.files/image384.gif) =2. … (12分)
=2. … (12分)
解法2:(Ⅰ)建立如图所示的空间直角坐标系,则卷.files/image350.gif) (0,0,1),M(0,
(0,0,1),M(0,卷.files/image386.gif) ,0),
,0),
C(0,1,0), A (卷.files/image388.gif) ),设N (0,1,a) ,所以,
),设N (0,1,a) ,所以,
卷.files/image390.gif) ,
,卷.files/image392.gif) ,
,卷.files/image394.gif)
因为卷.files/image396.gif) 所以
所以卷.files/image398.gif) ,同法可得
,同法可得卷.files/image400.gif) .又
.又卷.files/image402.gif) 故AM
故AM卷.files/image335.gif) 面BC
面BC卷.files/image404.gif)
卷.files/image350.gif) .
.
(II)由(Ⅰ)知?卷.files/image406.gif) ?为二面角
?为二面角卷.files/image350.gif) ―AM―N的平面角,以下同法一.
―AM―N的平面角,以下同法一.
21解(Ⅰ)由已知卷.files/image408.gif)
卷.files/image147.jpg) ∴
∴卷.files/image410.gif) ∴
∴卷.files/image412.gif) ………………(2分)
………………(2分)
又卷.files/image414.gif) 且
且卷.files/image416.gif) ∴
∴卷.files/image418.gif) (舍去
(舍去卷.files/image420.gif) )
)
∴卷.files/image422.gif) …(4分)
…(4分)
(Ⅱ)令卷.files/image424.gif) 即
即卷.files/image426.gif) 的增区间为
的增区间为卷.files/image428.gif) 、
、卷.files/image430.gif)
∵卷.files/image432.gif) 在区间
在区间卷.files/image434.gif) 上是增函数
上是增函数
∴卷.files/image436.gif) 或
或卷.files/image438.gif) 则
则卷.files/image440.gif) 或
或卷.files/image442.gif) ……(8分)
……(8分)
(Ⅲ)令卷.files/image444.gif) 或
或卷.files/image446.gif)
∵卷.files/image448.gif)
∴卷.files/image432.gif) 在
在卷.files/image451.gif) 上的最大值为4,最小值为0………………(10分)
上的最大值为4,最小值为0………………(10分)
∴卷.files/image453.gif) 、
、卷.files/image455.gif) 时,
时,卷.files/image457.gif) ……………(12分)
……………(12分)
22.解 (1)设卷.files/image459.gif) 为椭圆
为椭圆卷.files/image461.gif) 的左特征点,椭圆的左焦点为
的左特征点,椭圆的左焦点为卷.files/image463.gif) ,可设直线
,可设直线卷.files/image465.gif) 的方程为
的方程为卷.files/image467.gif) .并将它代入
.并将它代入卷.files/image461.gif) 得:
得:卷.files/image470.gif) ,即
,即卷.files/image472.gif) .设
.设卷.files/image474.gif) ,则
,则卷.files/image476.gif) ,……(3分)
,……(3分)
∵卷.files/image478.gif) 被
被卷.files/image366.gif) 轴平分,∴
轴平分,∴卷.files/image481.gif) .即
.即卷.files/image483.gif) .
.
即卷.files/image485.gif) ,∴
,∴卷.files/image487.gif) .……………(5分)
.……………(5分)
于是卷.files/image489.gif) .
.
∵卷.files/image491.gif) ,即
,即卷.files/image493.gif) .………………(7分)
.………………(7分)
(2)对于椭圆卷.files/image495.gif) .于是猜想:椭圆
.于是猜想:椭圆卷.files/image497.gif) 的“左特征点”是椭圆的左准线与
的“左特征点”是椭圆的左准线与卷.files/image366.gif) 轴的交点. ………………(9分)
轴的交点. ………………(9分)
卷.files/image147.jpg) 证明:设椭圆的左准线
证明:设椭圆的左准线卷.files/image500.gif) 与
与卷.files/image366.gif) 轴相交于M点,过A,B分别作
轴相交于M点,过A,B分别作卷.files/image500.gif) 的垂线,垂足分别为C,D.
的垂线,垂足分别为C,D.
据椭圆第二定义:卷.files/image504.gif) ∵
∵卷.files/image506.gif)
卷.files/image508.gif)
于是卷.files/image510.gif) 即
即卷.files/image512.gif) .∴
.∴卷.files/image514.gif) ,又
,又卷.files/image516.gif) 均为锐角,∴
均为锐角,∴卷.files/image518.gif) ,∴
,∴卷.files/image520.gif) .
.
∴卷.files/image522.gif) 的平分线.故M为椭圆的“左特征点”. ………(14分)
的平分线.故M为椭圆的“左特征点”. ………(14分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com