
题目列表(包括答案和解析)
(本小题满分12分)某个高中研究性学习小组共有9名学生,其中有3名男生和6名女生. 在研究学习过程中,要进行两次汇报活动(即开题汇报和结题汇报),每次汇报都从这9名学生中随机选1人作为代表发言. 设每人每次被选中与否均互不影响.
(Ⅰ)求两次汇报活动都由小组成员甲发言的概率;
(Ⅱ)设![]() 为男生发言次数与女生发言次数之差的绝对值,求
为男生发言次数与女生发言次数之差的绝对值,求![]() 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)某个高中研究性学习小组共有9名学生,其中有3名男生和6名女生. 在研究学习过程中,要进行两次汇报活动(即开题汇报和结题汇报),每次汇报都从这9名学生中随机选1人作为代表发言. 设每人每次被选中与否均互不影响.
(Ⅰ)求两次汇报活动都由小组成员甲发言的概率;
(Ⅱ)设![]() 为男生发言次数与女生发言次数之差的绝对值,求
为男生发言次数与女生发言次数之差的绝对值,求![]() 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
某市有A、B两所示范高中响应政府号召,对该市甲、乙两个教育落后地区开展支教活动.经上级研究决定:向甲地派出3名A校教师和2名B校教师,向乙地派出3名A校教师和3名B校教师.由于客观原因,需从拟派往甲、乙两地的教师中各自任选一名互换支教地区.
(Ⅰ)求互换后两校派往两地区教师人数不变的概率;
(Ⅱ)求互换后A校教师派往甲地人数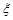 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
某研究机构为了研究人的体重与身高之间的关系,随机抽测了20人,得到如下数据:
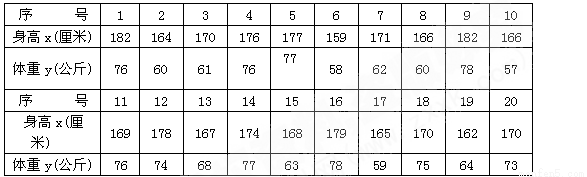
(1)若“身高大于175厘米”的为 “高个”,“身高小于等于175厘米”的为“非高个”;“体重大于75(公斤)”的为“胖子”,“体重小于等于75(公斤)”的为“非胖子”.请根据上表数据完成下面的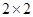 联列表:
联列表:
|
|
高 个 |
非高个 |
合 计 |
|
胖 子 |
|
|
|
|
非胖子 |
|
12 |
|
|
合 计 |
|
|
20 |
(2)根据题(1)中表格的数据,若按99%的可靠性要求,能否认为体重与身高之间有关系?
 2分)
2分) 乙地派出3名A校教师和3名B校教师.由于客观原因,需从拟派往甲、乙两地的教师中各自任选一名互换支教地区.
乙地派出3名A校教师和3名B校教师.由于客观原因,需从拟派往甲、乙两地的教师中各自任选一名互换支教地区. 的分布列和数学期望
的分布列和数学期望 .
.高三数学试卷(理科) 2009.4
题号
1
2
3
4
5
6
7
8
答案
C
B
A
B
C
C
D
A
一、选择题:本大题共 8 小题,每小题 5 分,共 40 分.
二、填空题:本大题共 6 小题,每小题 5 分,共 30 分.
9.
 10. 10,243 11.
10. 10,243 11.  12.
12.  13. 24 14.
13. 24 14. 
注:两空的题目,第一个空3分,第二个空2分.
三、解答题:本大题共 6 小题,共 80 分.
15.(本小题满分12分)
(Ⅰ)解:记 “2次汇报活动都是由小组成员甲发言” 为事件A. -----------------------------1分
由题意,得事件A的概率 ,
,
即2次汇报活动都是由小组成员甲发言的概率为 .
---------------------------5分
.
---------------------------5分
(Ⅱ)解:由题意,ξ的可能取值为2,0, ----------------------------6分
每次汇报时,男生被选为代表的概率为 ,女生被选为代表的概率为
,女生被选为代表的概率为 .
.
 ;
;  ;
;
所以, 的分布列为:
的分布列为:

2
0
P


---------------------------10分
 的数学期望
的数学期望 .
---------------------------12分
.
---------------------------12分
16.(本小题满分12分)
(Ⅰ)解:由三角函数的定义,得点B的坐标为 . ---------------------------1分
. ---------------------------1分
在 中,|OB|=2,
中,|OB|=2, ,
,
由正弦定理,得 ,即
,即 ,
,
所以  .
---------------------------5分
.
---------------------------5分
注:仅写出正弦定理,得3分. 若用直线AB方程求得 也得分.
也得分.
(Ⅱ)解:由(Ⅰ)得 , ------------------7分
, ------------------7分
因为 ,
,
所以 ,
----------------------------9分
,
----------------------------9分
又

 ,
---------------------------11分
,
---------------------------11分
所以 .
---------------------------12分
.
---------------------------12分
17.(本小题满分14分)
(Ⅰ)证明:在 中,
中, ,
,
 ,
,
 ,即
,即 ,
---------------------------1分
,
---------------------------1分
 ,
,
 平面
平面 .
---------------------------4分
.
---------------------------4分
(Ⅱ)方法一:
解:由(Ⅰ)知 ,
,
又 ,
,
 平面
平面 ,
---------------------------5分
,
---------------------------5分
如图,过C作 于M,连接BM,
于M,连接BM,
 是BM在平面PCD内的射影,
是BM在平面PCD内的射影,
 ,
,
又
 为二面角B-PD-C的平面角.
---------------------------7分
为二面角B-PD-C的平面角.
---------------------------7分
在 中,
中,  , PC=1,
, PC=1,  ,
,

 ,
,
又 ,
, ,
,
 . ---------------8分
. ---------------8分
在 中,
中,  , BC=1,
, BC=1,  ,
,
 ,
,
 二面角B-PD-C的大小为
二面角B-PD-C的大小为 .
---------------------------9分
.
---------------------------9分
方法二:
解:如图,在平面ABCD内,以C为原点, CD、CB、CP分别为x、y、z轴,建立空间直角坐标系C-xyz,
则 ,
---------------------------5分
,
---------------------------5分
过C作 于M,连接BM,设
于M,连接BM,设 ,
,
 则
则 ,
,
 ,
,
 ;
1
;
1
 共线,
共线,
 ,
2
,
2
由12,解得 ,
,
 点的坐标为
点的坐标为 ,
, ,
, ,
,
 ,
,
 ,
,
又 ,
,
 为二面角B-PD-C的平面角.
---------------------------7分
为二面角B-PD-C的平面角.
---------------------------7分
 ,
, ,
,
 ,
,
 二面角B-PD-C的大小为
二面角B-PD-C的大小为 .
--------------------------9分
.
--------------------------9分
(Ⅲ)解:设点B到平面PAD的距离为h,
 ,
, ,
,
 平面ABCD,
平面ABCD, ,
,
 ,
,
在直角梯形ABCD中, ,
,
 .
.
在 中,
中, ,
, ,
,

 ,
,
 ,
,
 的面积
的面积 ,
---------------------------10分
,
---------------------------10分
 三棱锥B-PAD的体积
三棱锥B-PAD的体积 ,
,

 ,
---------------------------12分
,
---------------------------12分
即 ,解得
,解得 ,
,
 点B到平面PAD的距离为
点B到平面PAD的距离为 .
---------------------------14分
.
---------------------------14分
18.(本小题满分14分)
(Ⅰ)解:函数 的定义域为
的定义域为 ,
---------------------------1分
,
---------------------------1分

 .
---------------------------4分
.
---------------------------4分
因为 ,所以
,所以 .
---------------------------5分
.
---------------------------5分
(Ⅱ)解:当 时,因为
时,因为 ,
,
所以 ,故
,故 在
在 上是减函数; ------------------------7分
上是减函数; ------------------------7分
当a=0时,当 时,
时, ,故
,故 在
在 上是减函数,
上是减函数,
当 时,
时, ,故
,故 在
在 上是减函数,
上是减函数,
因为函数 在
在 上连续,
上连续,
所以 在
在 上是减函数;
---------------------------9分
上是减函数;
---------------------------9分
当0<a<1时,由 , 得x=
, 得x= ,或x=
,或x= . --------------------------10分
. --------------------------10分
x变化时, 的变化如情况下表:
的变化如情况下表:








0
+
0



极小值

极大值

所以 在
在 上为减函数、在
上为减函数、在 上为减函数;
上为减函数; 在
在 上为增函数.
------------------------13分
上为增函数.
------------------------13分
综上,当 时,
时, 在
在 上是减函数;
上是减函数;
当0<a<1时, 在
在 上为减函数、在
上为减函数、在 上为减函数;
上为减函数; 在
在 上为增函数.
------------------------14分
上为增函数.
------------------------14分
19.(本小题满分14分)
(Ⅰ)解:设A(x1, y1),
因为A为MN的中点,且M的纵坐标为3,N的纵坐标为0,
所以 ,
---------------------------1分
,
---------------------------1分
又因为点A(x1, y1)在椭圆C上
所以 ,即
,即 ,解得
,解得 ,
,
则点A的坐标为 或
或 ,
-------------------------3分
,
-------------------------3分
所以直线l的方程为 或
或 . --------------------------5分
. --------------------------5分
(Ⅱ)解:设直线AB的方程为 或
或 ,A(x1, y1),B(x2, y2),
,A(x1, y1),B(x2, y2), ,
,
当AB的方程为 时,
时, ,与题意不符.
--------------------------6分
,与题意不符.
--------------------------6分
当AB的方程为 时:
时:
由题设可得A、B的坐标是方程组 的解,
的解,
消去y得 ,
,
所以 即
即 ,
,
则 ,
,
---------------------------8分
因为 
 ,
,
所以 ,解得
,解得 ,
,
所以 .
--------------------------10分
.
--------------------------10分
因为 ,即
,即 ,
,
所以当 时,由
时,由 ,得
,得 ,
,
上述方程无解,所以此时符合条件的直线 不存在; --------------------11分
不存在; --------------------11分
当 时,
时, ,
, ,
,
因为点 在椭圆上,
在椭圆上,
所以
 ,
-------------------------12分
,
-------------------------12分
化简得 ,
,
因为 ,所以
,所以 ,
,
则 .
.
综上,实数 的取值范围为
的取值范围为 .
---------------------------14分
.
---------------------------14分
20.(本小题满分14分)
(Ⅰ)解:由题意,创新数列为3,4,4,5,5的数列 有两个,即:
有两个,即:
(1)数列3,4,1,5,2; ---------------------------2分
(2)数列3,4,2,5,1. ---------------------------3分
注:写出一个得2分,两个写全得3分.
(Ⅱ)答:存在数列 ,它的创新数列为等差数列.
,它的创新数列为等差数列.
解:设数列 的创新数列为
的创新数列为 ,
,
因为 为
为 中的最大值.
中的最大值.
所以 .
.
由题意知: 为
为 中最大值,
中最大值, 为
为 中最大值,
中最大值,
所以 ,且
,且 .
.
若 为等差数列,设其公差为d,则
为等差数列,设其公差为d,则 ,且
,且 N, -----------------5分
N, -----------------5分
当d=0时, 为常数列,又
为常数列,又 ,
,
所以数列 为
为 ,此时数列
,此时数列 是首项为m的任意一个符合条件的数列;
是首项为m的任意一个符合条件的数列;
当d=1时,因为 ,
,
所以数列 为
为 ,此时数列
,此时数列 是
是 ; --------------------7分
; --------------------7分
当 时,因为
时,因为 ,
,
又 ,所以
,所以 ,
,
这与 矛盾,所以此时
矛盾,所以此时 不存在,即不存在
不存在,即不存在 使得它的创新数列为
使得它的创新数列为 的等差数列.
的等差数列.
综上,当数列 为:(1)首项为m的任意符合条件的数列;(2)数列
为:(1)首项为m的任意符合条件的数列;(2)数列 时,它的创新数列为等差数列.
时,它的创新数列为等差数列.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com