
题目列表(包括答案和解析)
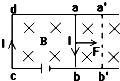 匀强磁场B中有一闭合电路abcd,其电流I保持不变,为L的导线ab可以沿光滑导轨dacb滑动,从ab滑到a′b′,导线在移动过程中,扫过的回路面积增量为△S,则安培力所做的功是( )
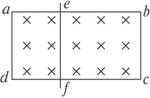
匀强磁场B中有一闭合电路abcd,其电流I保持不变,为L的导线ab可以沿光滑导轨dacb滑动,从ab滑到a′b′,导线在移动过程中,扫过的回路面积增量为△S,则安培力所做的功是( )如图1所示,矩形金属框置于匀强磁场中,ef为一导体棒,可在ab和cd间滑动并接触良好;设磁感应强度为B,ef长为L,在Δt时间内向左匀速滑过距离Δd,由电磁感应定律E=n 可知,下列说法正确的是(
)
可知,下列说法正确的是(
)

图1
A、当ef向左滑动时,左侧面积减少L·Δd,右侧面积增加L·Δd,因此E=2BLΔd/Δt
B、当ef向左滑动时,左侧面积减小L·Δd,右侧面积增大L·Δd,互相抵消,因此E=0
C、在公式 中,在切割情况下,ΔΦ=B·ΔS,ΔS应是导线切割扫过的面积,因此E=BLΔd/Δt
中,在切割情况下,ΔΦ=B·ΔS,ΔS应是导线切割扫过的面积,因此E=BLΔd/Δt
D、在切割的情况下,只能用E=BLv计算,不能用 计算
计算
图
A.当ef向右滑动时,左边的面积增大lΔd,右边的面积减少lΔd,电动势应为E=![]()
B.当ef向右滑动时,左边的面积增大lΔd,右边的面积减少lΔd,相互抵消E=0
C.在公式E=![]() 中,切割磁感线的情况下ΔΦ=BΔS,ΔS应为导线切割扫过的面积,故有E=
中,切割磁感线的情况下ΔΦ=BΔS,ΔS应为导线切割扫过的面积,故有E=![]()
D.在切割磁感线的情况下只能用E=Blv来计算,不能用E=![]() 来计算
来计算
如图16-2-6所示,矩形金属框置于匀强磁场中,ef为一导体棒,可在ab和cd间滑动并接触良好,设磁感应强度为B,ef长为L,在Δt时间内向左匀速滑过距离Δd,由电磁感应定律E=![]() 可知,下列说法正确的是( )
可知,下列说法正确的是( )

图16-2-6
A.当ef向左滑动时,左侧面积减小L·Δd,右侧面积增大L·Δd,因此E=2BLΔd/Δt
B.当ef向左滑动时,左侧面积减小L·Δd,右侧面积增大L·Δd,互相抵消,因此E=0
C.在公式E=![]() 中,在切割情况下,ΔΦ=B·ΔS,ΔS应是导线切割扫过的面积,因此E=BLΔd/Δt
中,在切割情况下,ΔΦ=B·ΔS,ΔS应是导线切割扫过的面积,因此E=BLΔd/Δt
D.在切割的情况下,只能用E=BLv计算,不能用E=![]() 计算
计算

图
A.当ef向左滑动时,左侧面积减小L·Δd,右侧面积增大L·Δd,因此E=2BLΔd/Δt
B.当ef向左滑动时,左侧面积减小L·Δd,右侧面积增大L·Δd,互相抵消,因此E=0
C.在公式E=![]() 中,在切割情况下,ΔΦ=B·ΔS,ΔS应是导线切割扫过的面积,因此E=BLΔd/Δt
中,在切割情况下,ΔΦ=B·ΔS,ΔS应是导线切割扫过的面积,因此E=BLΔd/Δt
D.在切割的情况下,只能用E=BLv计算,不能用E=![]() 计算
计算
 1.B.提示:将圆环转换为并联电源模型,如图
1.B.提示:将圆环转换为并联电源模型,如图
2.CD 3.AD
4.Q=IΔt= 或Q=
或Q=
5.(1)3.2×10-2 N (2)1.28×10-2 J
提示:将电路转换为直流电路模型如图. 
6.(1)电压表 理由略
(2)F=1.6 N (3)Q=
7.(1)如图所示,当EF从距BD端s处由静止开始滑至BD的过程中,受力情况如图所示.安培力:F安=BIl=B

根据牛顿第二定律:a= ①
①
所以,EF由静止开始做加速度减小的变加速运动.当a=0时速度达到最大值vm.
由①式中a=0有:Mgsinθ-B
vm=
(2)由恒力F推至距BD端s处,棒先减速至零,然后从静止下滑,在滑回BD之前已达最大速度vm开始匀速.
设EF棒由BD从静止出发到再返回BD过程中,转化成的内能为ΔE.根据能的转化与守恒定律:
Fs-ΔE= Mvm2 ③
Mvm2 ③
ΔE=Fs- M(
M( )2 ④
)2 ④
8.(1)每半根导体棒产生的感应电动势为
E1=Bl =
= Bl2ω=
Bl2ω= ×0.4×103×(0.5)2 V=50 V.
×0.4×103×(0.5)2 V=50 V.
(2)两根棒一起转动时,每半根棒中产生的感应电动势大小相同、方向相同(从边缘指向中心),相当于四个电动势和内阻相同的电池并联,得总的电动势和内电阻
为E=E1=50 V,r= R0=0.1 Ω
R0=0.1 Ω
当电键S断开时,外电路开路,电流表示数为零,电压表示数等于电源电动势,为50 V.
当电键S′接通时,全电路总电阻为
R′=r+R=(0.1+3.9)Ω=4Ω.
由全电路欧姆定律得电流强度(即电流表示数)为
I= A=
A=
此时电压表示数即路端电压为
U=E-Ir=50-12.5×0.1 V=48.75 V(电压表示数)
或U=IR=12.5×3.9 V=48.75 V
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com