解析　(1)小球从曲面上滑下，只有重力做功，由机械能守恒定律知：

mgh＝mv                                                       ①

得v₀＝＝ m/s＝2 m/s.

(2)小球离开平台后做平抛运动，小球正好落在木板的末端，则

H＝gt²                                                                                                                                                      ②

＝v₁t                                                                                                                ③

联立②③两式得：v₁＝4 m/s

设释放小球的高度为h₁，则由mgh₁＝mv

得h₁＝＝0.8 m.

(3)由机械能守恒定律可得：mgh＝mv²

小球由离开平台后做平抛运动，可看做水平方向的匀速直线运动和竖直方向的自由落体运动，则：

y＝gt²                                                                                                                                                       ④

x＝vt                                                                                                                       ⑤

tan 37°＝                                                                                                          ⑥

v_y＝gt                                                                                                                      ⑦

v＝v²＋v                                                       ⑧

E_k＝mv                                                      ⑨

由④⑤⑥⑦⑧⑨式得：E_k＝32.5h                                                                       ⑩

考虑到当h>0.8 m时小球不会落到斜面上，其图象如图所示

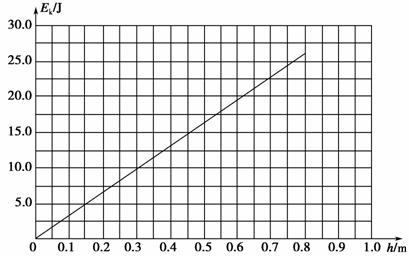
答案　(1)2 m/s　(2)0.8 m　(3)E_k＝32.5h　图象见解析

如图所示，一质量为M的物块静止在桌面边缘，桌面离水平地面的高度为h.一质量为m的子弹以水平速度v₀射入物块后，以水平速度v₀/2射出．重力加速度为g.求：

(1)此过程中系统损失的机械能；

(2)此后物块落地点离桌面边缘的水平距离．

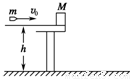
【解析】：(1)设子弹穿过物块后物块的速度为v，由动量守恒得mv₀＝m＋Mv①

解得v＝v₀②

系统的机械能损失为

ΔE＝mv－[m()²＋Mv²]③

由②③式得ΔE＝(3－)mv.④

(2)设物块下落到地面所需时间为t，落地点距桌面边缘的水平距离为s，则h＝gt²⑤

s＝vt⑥

由②⑤⑥式得s＝.

如图所示，一质量为M的物块静止在桌面边缘，桌面离水平地面的高度为h.一质量为m的子弹以水平速度v₀射入物块后，以水平速度v₀/2射出．重力加速度为g.求：

(1)此过程中系统损失的机械能；

(2)此后物块落地点离桌面边缘的水平距离．

【解析】：(1)设子弹穿过物块后物块的速度为v，由动量守恒得mv₀＝m＋Mv①

解得v＝v₀②

系统的机械能损失为

ΔE＝mv－[m()²＋Mv²]③

由②③式得ΔE＝(3－)mv.④

(2)设物块下落到地面所需时间为t，落地点距桌面边缘的水平距离为s，则h＝gt²⑤

s＝vt⑥

由②⑤⑥式得s＝.