巢湖市教育局规定:初中升学须进行体育考试.总分30分.成绩计入初中毕业升学考试总分.还将作为初中毕业生综合素质评价“运动和健康维度的实证材料．为了解九年级学生的体育素质.某校从九年级的六个班级共4——青夏教育精英家教网—

巢湖市教育局规定:初中升学须进行体育考试.总分30分.成绩计入初中毕业升学考试总分.还将作为初中毕业生综合素质评价“运动和健康维度的实证材料．为了解九年级学生的体育素质.某校从九年级的六个班级共420名学生中按分层抽样抽取60名学生进行体育素质测试．班现有学生70人.按分层抽样.则九(1)班应抽取学生多少人?.(2)班所抽取学生的体育测试成绩的茎叶图【查看更多】

(本小题满分12分)

在股票市场上，投资者常参考股价（每一股的价格）的某条平滑均线（记作MA）的变化情况来决定买入或卖出股票。股民老赵在研究股票的走势图时，发现一只股票的MA均线近期走得很有特点：如果按如图所示的方式建立平面直角坐标系xoy，则股价y（元）和时间x的关系在ABC段可近似地用解析式来描述，从C点走到今天的D点，是震荡筑底阶段，而今天出现了明显的筑底结束的标志，且D点和C点正好关于直线对称。老赵预计这只股票未来的走势如图中虚线所示，这里DE段与ABC段关于直线对称，EF段是股价延续DE段的趋势（规律）走到这波上升行情的最高点F。现在老赵决定取点，点，点来确定解析式中的常数，并且已经求得。

（1）请你帮老赵算出，并回答股价什么时候见顶（即求F点的横坐标）；

（2）老赵如能在今天以D点处的价格买入该股票5000股，到见顶处F点的价格全部卖出，不计其它费用，这次操作他能赚多少元？

查看答案和解析>>

（本小题满分12分）根据市气象站对春季某一天气温变化的数据统计显示，气温变化的分布可以用曲线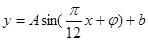拟合（，单位为小时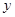，表示气温，单位为摄氏度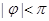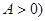，，，现已知这天气温为4至12摄氏度，并得知在凌晨1时整气温最低，下午13时整气温最高。

（1）求这条曲线的函数表达式；

（2）求这一天19时整的气温。

查看答案和解析>>

（本小题满分12分）

某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下表所示：

零件的个数（个）	2	3	4	5
加工的时间（小时）	2.5	3	4	4.5

（Ⅰ）在给定的坐标系中画出表中数据的散点图；

（Ⅱ）求出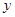关于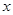的线性回归方程，

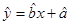并在坐标系中画出回归直线；

（Ⅲ）试预测加工10个零件需要多少时间？

查看答案和解析>>

（本小题满分12分）根据市气象站对春季某一天气温变化的数据统计显示，气温变化的分布可以用曲线拟合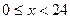（，单位为小时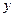，表示气温，单位为摄氏度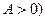，，，现已知这天气温为4至12摄氏度，并得知在凌晨1时整气温最低，下午13时整气温最高。
（1）求这条曲线的函数表达式；
（2）求这一天19时整的气温。

查看答案和解析>>

（本小题满分12分）

某市电信部门规定：拨打本市电话时，如果通话时间不超过3分钟，则收取通话费0.2元；如果通话时间超过3分钟，则超过部分以0.1元/分钟收取通话费（时间以分钟计，不足1分钟按1分钟计）。现设计了一个计算通话费用的算法：

S1 输入通话时间（按题目要求取整数）；

S2 如果，则，否则；w。w-w*k&s%5￥u

S3 输出费用

（1）试写出该算法的一个程序框图；

（2）表1为A、B、C、D、E五人拨打本市电话的情况，将A、C的应缴话费数填入表1中适当位置；

表1

	A	B	C	D	E
第一次通话时间	3分钟	3分45秒	3分55秒	3分20秒	6分钟
第二次通话时间	0分钟	4分钟	3分40秒	4分50秒	0分钟
第三次通话时间	0分钟	0分钟	5分钟	2分钟	0分钟
应缴话费（元）		0.60		0.90	0.50