
题目列表(包括答案和解析)
解:(1)如图①AH=AB
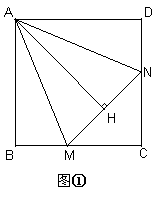 (2)数量关系成立.如图②,延长CB至E,使BE=DN
(2)数量关系成立.如图②,延长CB至E,使BE=DN
∵ABCD是正方形
∴AB=AD,∠D=∠ABE=90°
∴Rt△AEB≌Rt△AND
∴AE=AN,∠EAB=∠NAD
∴∠EAM=∠NAM=45°
∵AM=AM
∴△AEM≌△ANM
∵AB、AH是△AEM和△ANM对应边上的高,
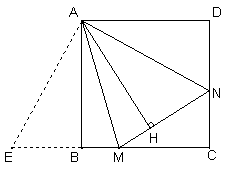 ∴AB=AH
∴AB=AH
(3)如图③分别沿AM、AN翻折△AMH和△ANH,
得到△ABM和△AND
∴BM=2,DN=3,∠B=∠D=∠BAD=90°
分别延长BM和DN交于点C,得正方形ABCE.
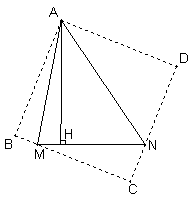 由(2)可知,AH=AB=BC=CD=AD.
由(2)可知,AH=AB=BC=CD=AD.
设AH=x,则MC=![]() , NC=
, NC=![]() 图②
图②
在Rt⊿MCN中,由勾股定理,得
![]()
∴![]()
解得![]() .(不符合题意,舍去)
.(不符合题意,舍去)
∴AH=6.
解:(1)如图,![]() 与
与![]() 互相垂直平分. (1分)
互相垂直平分. (1分)
证明如下:连结![]() 、
、![]() ,
,
∵![]() //
//![]() ,
,
∴四边形![]() 是平行四边形. (2分)
是平行四边形. (2分)
![]() ⊥
⊥![]() ,
,
∴![]() ⊥
⊥![]() ,
,
∵∠![]() =90º,
=90º,![]() 为
为![]() 的中点,
的中点,
∴![]() , (2分)
, (2分)
∴四边形![]() 是菱形. (1分)
是菱形. (1分)
∴![]() 与
与![]() 互相垂直平分.
互相垂直平分.
解:(2)设![]() ,则
,则![]() ,
,![]() . (2分)
. (2分)
在Rt△![]() 中,∵
中,∵![]() , (1分)
, (1分)
∴![]() . (1分)
. (1分)
![]()
![]() (1分)
(1分)
∴![]() . (2分)
. (2分)
解:(1)由抛物线C1:![]() 得顶点P的坐标为(2,5)………….1分
得顶点P的坐标为(2,5)………….1分
 ∵点A(-1,0)在抛物线C1上∴
∵点A(-1,0)在抛物线C1上∴![]() .………………2分
.………………2分
(2)连接PM,作PH⊥x轴于H,作MG⊥x轴于G..
∵点P、M关于点A成中心对称,
∴PM过点A,且PA=MA..
∴△PAH≌△MAG..
∴MG=PH=5,AG=AH=3.
∴顶点M的坐标为(![]() ,5).………………………3分
,5).………………………3分
∵抛物线C2与C1关于x轴对称,抛物线C3由C2平移得到
∴抛物线C3的表达式![]() . …………4分
. …………4分
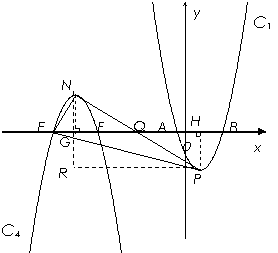
(3)∵抛物线C4由C1绕x轴上的点Q旋转180°得到
∴顶点N、P关于点Q成中心对称.
由(2)得点N的纵坐标为5.
设点N坐标为(m,5),作PH⊥x轴于H,作NG⊥x轴于G,作PR⊥NG于R.
∵旋转中心Q在x轴上,
∴EF=AB=2AH=6.
∴EG=3,点E坐标为(![]() ,0),H坐标为(2,0),R坐标为(m,-5).
,0),H坐标为(2,0),R坐标为(m,-5).
 根据勾股定理,得
根据勾股定理,得
![]()
![]()
![]()
①当∠PNE=90º时,PN2+ NE2=PE2,
解得m=![]() ,∴N点坐标为(
,∴N点坐标为(![]() ,5)
,5)
②当∠PEN=90º时,PE2+ NE2=PN2,
解得m=![]() ,∴N点坐标为(
,∴N点坐标为(![]() ,5).
,5).
③∵PN>NR=10>NE,∴∠NPE≠90º ………7分
综上所得,当N点坐标为(![]() ,5)或(
,5)或(![]() ,5)时,以点P、N、E为顶点的三角形是直角三角形.…………………………………………………………………………………8分
,5)时,以点P、N、E为顶点的三角形是直角三角形.…………………………………………………………………………………8分
解:(1)A(-1,0),B(3,0),C(0,3).·················· 2分
抛物线的对称轴是:x=1.······················· 3分
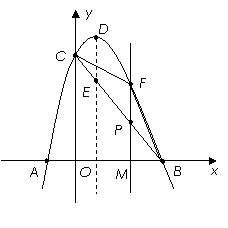 (2)①设直线BC的函数关系式为:y=kx+b.
(2)①设直线BC的函数关系式为:y=kx+b.
把B(3,0),C(0,3)分别代入得:
![]() 解得:k= -1,b=3.
解得:k= -1,b=3.
所以直线BC的函数关系式为:![]() .
.
当x=1时,y= -1+3=2,∴E(1,2).
当![]() 时,
时,![]() ,
,
∴P(m,![]() m+3).·························· 4分
m+3).·························· 4分
在![]() 中,当
中,当![]() 时,
时,![]()
∴![]()
当![]() 时,
时,![]() ∴
∴![]() ········· 5分
········· 5分
∴线段DE=4-2=2,线段![]() ···· 6分
···· 6分
∵![]()
∴当![]() 时,四边形
时,四边形![]() 为平行四边形.
为平行四边形.
由![]() 解得:
解得:![]() (不合题意,舍去).
(不合题意,舍去).
因此,当![]() 时,四边形
时,四边形![]() 为平行四边形.··········· 7分
为平行四边形.··········· 7分
②设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,由
,由![]() 可得:
可得:![]()
∵![]() ························ 8分
························ 8分
即![]() .
.
![]()
![]() ·········· 9分
·········· 9分
解:(1)点C的坐标为![]() .
.
∵ 点A、B的坐标分别为![]() ,
,
∴ 可设过A、B、C三点的抛物线的解析式为![]() .
.
将![]() 代入抛物线的解析式,得
代入抛物线的解析式,得![]() .
.
∴ 过A、B、C三点的抛物线的解析式为![]() .
.
 (2)可得抛物线的对称轴为
(2)可得抛物线的对称轴为![]() ,顶点D的坐标为
,顶点D的坐标为
![]() ,设抛物线的对称轴与x轴的交点为G.
,设抛物线的对称轴与x轴的交点为G.
直线BC的解析式为![]() .
.
设点P的坐标为![]() .
.
解法一:如图8,作OP∥AD交直线BC于点P,
连结AP,作PM⊥x轴于点M.
∵ OP∥AD,
∴ ∠POM=∠GAD,tan∠POM=tan∠GAD.
∴ ![]() ,即
,即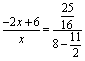 .
.
解得![]() . 经检验
. 经检验![]() 是原方程的解.
是原方程的解.
此时点P的坐标为![]() .
.
但此时![]() ,OM<GA.
,OM<GA.
∵ ![]()
∴ OP<AD,即四边形的对边OP与AD平行但不相等,
∴ 直线BC上不存在符合条件的点P. - - - - - - - - - - - - - - - - - - - - - 6分
解法二:如图9,取OA的中点E,作点D关于点E的对称点P,作PN⊥x轴于
点N. 则∠PEO=∠DEA,PE=DE.
可得△PEN≌△DEG .
由![]() ,可得E点的坐标为
,可得E点的坐标为![]() .
.
NE=EG=![]() , ON=OE-NE=
, ON=OE-NE=![]() ,NP=DG=
,NP=DG=![]() .
.
∴ 点P的坐标为![]() .∵ x=
.∵ x=![]() 时,
时,![]() ,
,
∴ 点P不在直线BC上.
∴ 直线BC上不存在符合条件的点P .

(3)![]() 的取值范围是
的取值范围是![]() .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com