
题目列表(包括答案和解析)
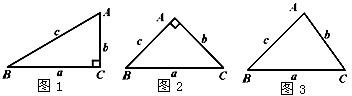
如图1,在ΔABC中,∠A=2∠B,且∠A=60°.小明通过以下计算:由题意,∠B=30°,∠C=90°,c=2b,a=![]() b,得a2-b2=(
b,得a2-b2=(![]() b)2-b2=2b2=b?c.即a2-b2= bc.
b)2-b2=2b2=b?c.即a2-b2= bc.
于是,小明猜测:对于任意的ΔABC,当∠A=2∠B时,关系式a2-b2=bc都成立.
(1)如图2,请你用以上小明的方法,对等腰直角三角形进行验证,判断小明的猜测是否正确,并写出验证过程;
(2)如图3,你认为小明的猜想是否正确,若认为正确,请你证明;否则,请说明理由;
(3)若一个三角形的三边长恰为三个连续偶数,且∠A=2∠B,请直接写出这个三角形三边的长,不必说明理由.
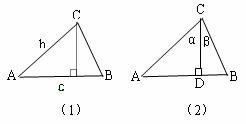
如下图(1),由直角三角形边角关系,可将三角形面积公式变形,
得 ![]() =
=![]() bc?sin∠A. ①
bc?sin∠A. ①
即三角形的面积等于两边之长与夹角正弦之积的一半.
如下图(2),在ABC中,CD⊥AB于D,∠ACD=α, ∠DCB=β.
∵ ![]() , 由公式①,得
, 由公式①,得
![]() AC?BC?sin(α+β)=
AC?BC?sin(α+β)= ![]() AC?CD?sinα+
AC?CD?sinα+![]() BC?CD?sinβ,
BC?CD?sinβ,
即 AC?BC?sin(α+β)= AC?CD?sinα+BC?CD?sinβ. ②
你能利用直角三角形边角关系,消去②中的AC、BC、CD吗?不能,说明理由;能,写出解决过程.
如图1,线段![]() 过圆心O,交圆O于A,B两点,PC切圆O于点C,作
过圆心O,交圆O于A,B两点,PC切圆O于点C,作![]() ,垂足为D,连结AC,BC。
,垂足为D,连结AC,BC。
(1)写出图1中所有相等的角(直角除外),并给出证明;
(2)若图1中的切线PC变为图2中割线PCE的情形,PCE与圆O交于C,E两点,AE与BC交于点M,![]() ,写出图2中相等的角(写出三组即可,直角除外);
,写出图2中相等的角(写出三组即可,直角除外);
(3)在图2中,证明:AD?AB=AC?AE。


我国东南沿海某地的风力资源丰富,一年内日平均风速不小于3米/秒的时间共约160天,其中日平均风速不小于6米/秒的时间约占60天。
为了充分利用“风能”这种“绿色能源”,该地拟建一个小型风力发电场,决定选用A、B两种型号的风力发电机。根据产品说明,这两种风力发电机在各种风速下的日发电量(即一天的发电量)如下表:
| 日平均风速 |
| 3≤ |
| |
| 日发电量(千瓦?时) | A型发电机 | 0 | ≥36 | ≥150 |
| B型发电机 | 0 | ≥24 | ≥90 | |
根据上面的数据回答:
(1)若这个发电场购![]() 台A型风力发电机,则预计这些A型风力发电机一年的发电总量至少为_____________千瓦?时;
台A型风力发电机,则预计这些A型风力发电机一年的发电总量至少为_____________千瓦?时;
(2)已知A型风力发电机每台0.3万元,B型风力发电机每台0.2万元,该发电机拟购置风力发电机共10台,希望购机的费用不超过2.6万元,而建成的风力发电场每年的发电总量不少于102000千瓦?时,请你提供符合条件的购机方案。
如图1,草原上有A,B,C三个互通公路的奶牛养殖基地,B与C之间距离为100千米,C在B的正北方,A在C的南偏东47°方向且在B的北偏东43°方向.A地每年产奶3万吨;B地有奶牛9 000头,平均每头牛的年产奶量为3吨;C地养了三种奶牛,其中黑白花牛的头数占20%,三河牛的头数占35%,其他情况反映在图2,图3中.
(1)通过计算补全图3;
(2)比较B地与C地中,哪一地平均每头牛的年产奶量更高?
(3)如果从B,C两地中选择一处建设一座工厂解决三个基地的牛奶加工问题,当运送一吨牛奶每千米的费用都为1元(即1元/吨?千米时,那么从节省运费的角度考虑,应在何处建设工厂?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com