
题目列表(包括答案和解析)
(本小题为选做题,满分8分)
用数学归纳法证明不等式:![]() .
.
已知等比数列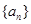 中,
中,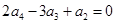 ,且
,且 ,公比
,公比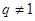 ,(1)求
,(1)求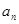 ;(2)设
;(2)设 ,求数列
,求数列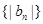 的前
的前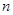 项和
项和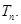
【解析】第一问,因为由题设可知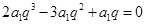
又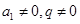 故
故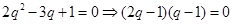
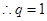 或
或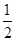 ,又由题设
,又由题设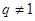
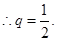 从而
从而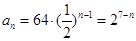
第二问中,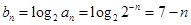
当 时,
时,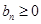 ,
, 时
时
故 时,
时,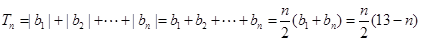
 时,
时,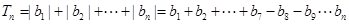
分别讨论得到结论。
由题设可知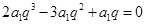
又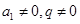 故
故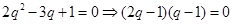
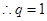 或
或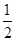 ,又由题设
,又由题设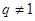
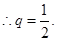
从而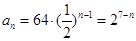 ……………………4分
……………………4分
(2)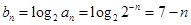
当 时,
时,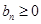 ,
, 时
时 ……………………6分
……………………6分
故 时,
时,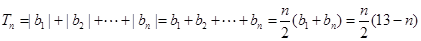 ……8分
……8分
 时,
时,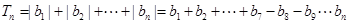
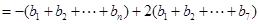
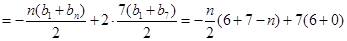
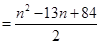 ……………………10分
……………………10分
综上可得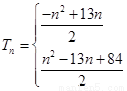

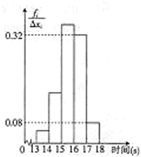 (2012•安徽模拟)为了了解某年级1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.
(2012•安徽模拟)为了了解某年级1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8. 为检查某工厂所产8万台电扇的质量,抽查了其中20台的无故障连续使用时限如下:
为检查某工厂所产8万台电扇的质量,抽查了其中20台的无故障连续使用时限如下:| 分 组 | 频数 | 频率 | 频率 组距 |
| [180,200) | |||
| [200,220) | |||
| [220,240) | |||
| [240,260) | |||
| [260,280) | |||
| [280,300) | |||
| [300,320) | |||
| [320,340] | |||
| 合 计 | 0.05 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com