
题目列表(包括答案和解析)
(08年扬州中学) 如图,在四棱锥P―ABC中,PA⊥底面ABCD,∠DAB=90°,AB∥CD,AD=CD=2AB=2,E、F分别为PC、CD的中点
⑴证明:CD⊥平面BEF;
⑵设PA=k?AB,且AD与PC所成的角为60°,求k的值.

下列四个命题中,正确命题有( )
①直线方程的一般式为Ax + By + C = 0 ②k1?k2 = 1为两直线垂直的充要条件
③k1 = k2为两直线平行的必要非充分条件 ④l:A1x + B1y + C1 = 0和l2:A2x + B2y + C2 = 0,(B1≠0,B2≠0,A1A2 + B1B2≠0),则直线l1到l2的角![]() 的正切值为
的正切值为![]()
A.0个 B.1个 C.2个 D.3个
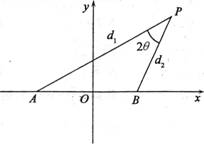 设动点P到点A(-l,0)和B(1,0)的距离分别为d1和d2,∠APB=2θ,且存在常数λ(0<λ<1),使得d1d2 sin2θ=λ.
设动点P到点A(-l,0)和B(1,0)的距离分别为d1和d2,∠APB=2θ,且存在常数λ(0<λ<1),使得d1d2 sin2θ=λ.
(1)证明:动点P的轨迹C为双曲线,并求出C的方程;
(2)过点B作直线交双曲线C的右支于M、N两点,试确定λ的范围,使![]() ?
?![]() =0,其中点O为坐标原点.
=0,其中点O为坐标原点.
在![]() 中,
中,![]() 的对边分别是
的对边分别是![]() ,且满足
,且满足![]() .
.
(1)求![]() 的大小;
的大小;
(2)设m![]() ,n
,n![]()
![]() ,且m?n的最大值是5,求
,且m?n的最大值是5,求![]() 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com