
题目列表(包括答案和解析)
对于x,符号[x]表示不超过x的最大整数,例如[π]=3,[-1.08]=-2,定义函数f(x)=x-[x],则下列命题中正确的是
f(3)=1
方程f(x)=![]() 有且仅有一解
有且仅有一解
f(x+1)=f(x)
若x1<x2,则f(x1)<f(x2)
为配合客户不同需要,某通信公司有下表所列的
A、B两种优惠计划供客户选择:
请根据上面提供的信息,解答下面的问题:
(1)
设通话时间为x分钟,所需付出的费用为y元,分别写出计划A、计划B中y与x之间的函数关系式.(2)
通话时间超过多少分钟时,计划B才会比计划A更省钱?(3)
若用户决定选择计划B,则通话多少时间,可以比选择计划A便宜,最多便宜多少钱?(4)
建立直角坐标系,画出A、B两种计划所对应的函数图象.(5)
通过以上研究,你觉得应该如何选择电信部门为客户提供的“优惠计划”?为配合客户不同需要,某通信公司有下表所列的A、B两种优惠计划供客户选择:
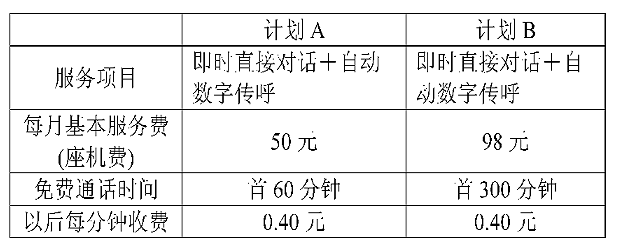
请根据上面提供的信息,解答下面的问题:
(1)设通话时间为x分钟,所需付出的费用为y元,分别写出计划A、计划B中y与x之间的函数关系式.
(2)通话时间超过多少分钟时,计划B才会比计划A更省钱?
(3)若用户决定选择计划B,则通话多少时间,可以比选择计划A便宜,最多便宜多少钱?
(4)建立直角坐标系,画出A、B两种计划所对应的函数图象.
(5)通过以上研究,你觉得应该如何选择电信部门为客户提供的“优惠计划”?
探究函数![]() ,x∈(0,+∞)的最小值,并确定相应的x的值,列表如下:
,x∈(0,+∞)的最小值,并确定相应的x的值,列表如下:
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | … |
请观察表中y值随x值变化的特点,完成下列问题:
(1)若函数![]() ,(x>0)在区间(0,2)上递减,则在 上递增;
,(x>0)在区间(0,2)上递减,则在 上递增;
(2)当x= 时,![]() ,(x>0)的最小值为 ;
,(x>0)的最小值为 ;
(3)试用定义证明![]() ,(x>0)在区间(0,2)上递减;
,(x>0)在区间(0,2)上递减;
(4)函数![]() ,(x<0)有最值吗?是最大值还是最小值?此时x为何值?
,(x<0)有最值吗?是最大值还是最小值?此时x为何值?
(5)解不等式![]() .
.
解题说明:(1)(2)两题的结果直接填写在横线上;(4)题直接回答,不需证明。
 ,x∈(0,+∞)的最小值,并确定相应的x的值,列表如下:
,x∈(0,+∞)的最小值,并确定相应的x的值,列表如下:| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | … |
 ,(x>0)在区间(0,2)上递减,则在 上递增;
,(x>0)在区间(0,2)上递减,则在 上递增; ,(x>0)的最小值为 ;
,(x>0)的最小值为 ; ,(x>0)在区间(0,2)上递减;
,(x>0)在区间(0,2)上递减; ,(x<0)有最值吗?是最大值还是最小值?此时x为何值?
,(x<0)有最值吗?是最大值还是最小值?此时x为何值? .
.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com