
题目列表(包括答案和解析)
已知m>1,直线 ,椭圆C:
,椭圆C: ,
, 、
、 分别为椭圆C的左、右焦点.
分别为椭圆C的左、右焦点.
(Ⅰ)当直线过右焦点 时,求直线的方程;
时,求直线的方程;
(Ⅱ)设直线与椭圆C交于A、B两点,△A
 、△B
、△B
 的重心分别为G、H.若原点O在以线段GH为直径的圆内,求实数m的取值范围.[
的重心分别为G、H.若原点O在以线段GH为直径的圆内,求实数m的取值范围.[
【解析】第一问中因为直线 经过点
经过点 (
( ,0),所以
,0),所以 =
= ,得
,得 .又因为m>1,所以
.又因为m>1,所以 ,故直线的方程为
,故直线的方程为
第二问中设 ,由
,由 ,消去x,得
,消去x,得 ,
,
则由 ,知
,知 <8,且有
<8,且有
由题意知O为
 的中点.由
的中点.由 可知
可知 从而
从而 ,设M是GH的中点,则M(
,设M是GH的中点,则M( ).
).
由题意可知,2|MO|<|GH|,得到范围
某高中地处县城,学校规定家到学校的路程在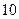 里
里
以内的学生可以走读,因交通便利,所以走读生人数很多,
该校学生会先后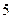 次对走读生的午休情况作了统计,得到
次对走读生的午休情况作了统计,得到
如下资料:
①若把家到学校的距离分为五个区间: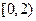 、
、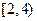 、
、 、
、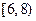 、
、 ,则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如右图所示的频率分布直方图;
,则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如右图所示的频率分布直方图;
②走读生是否午休与下午开始上课的时间有着密切的关系. 下表是根据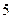 次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表.
次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表.
| 下午开始上课时间 | 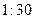 |  | 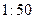 | 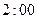 | 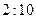 |
| 平均每天午休人数 |  |  | 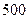 | 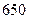 |  |
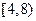 的概率是多少?
的概率是多少?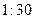 作为横坐标
作为横坐标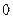 ,然后上课时间每推迟
,然后上课时间每推迟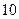 分钟,横坐标
分钟,横坐标 增加2,并以平均每天午休人数作为纵坐标
增加2,并以平均每天午休人数作为纵坐标 ,试列出
,试列出 与
与 的统计表,并根据表中的数据求平均每天午休人数
的统计表,并根据表中的数据求平均每天午休人数 与上课时间
与上课时间 之间的线性回归方程
之间的线性回归方程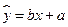 ;
; 时,家距学校的路程在4里路以下的走读生中约有多少人午休?
时,家距学校的路程在4里路以下的走读生中约有多少人午休?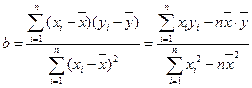 )
)某高中地处县城,学校规定家到学校的路程在 里
里
以内的学生可以走读,因交通便利,所以走读生人数很多,
该校学生会先后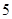 次对走读生的午休情况作了统计,得到
次对走读生的午休情况作了统计,得到
如下资料:
①若把家到学校的距离分为五个区间: 、
、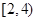 、
、 、
、 、
、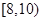 ,则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如右图所示的频率分布直方图;
,则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如右图所示的频率分布直方图;
②走读生是否午休与下午开始上课的时间有着密切的关系. 下表是根据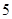 次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表.
次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表.
|
下午开始上课时间 |
|
|
|
|
|
|
平均每天午休人数 |
|
|
|
|
|
(Ⅰ)若随机地调查一位午休的走读生,其家到学校的路程(单位:里)在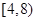 的概率是多少?
的概率是多少?
(Ⅱ)如果把下午开始上课时间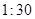 作为横坐标
作为横坐标 ,然后上课时间每推迟
,然后上课时间每推迟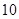 分钟,横坐标
分钟,横坐标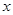 增加2,并以平均每天午休人数作为纵坐标
增加2,并以平均每天午休人数作为纵坐标 ,试列出
,试列出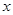 与
与 的统计表,并根据表中的数据求平均每天午休人数
的统计表,并根据表中的数据求平均每天午休人数 与上课时间
与上课时间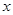 之间的线性回归方程
之间的线性回归方程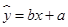 ;
;
(Ⅲ)预测当下午上课时间推迟到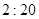 时,家距学校的路程在4里路以下的走读生中约有多少人午休?
时,家距学校的路程在4里路以下的走读生中约有多少人午休?
(注:线性回归直线方程系数公式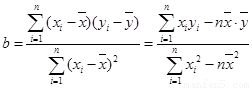 )
)
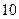 里
里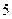 次对走读生的午休情况作了统计,得到
次对走读生的午休情况作了统计,得到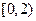 、
、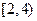 、
、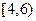 、
、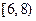 、
、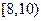 ,则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如右图所示的频率分布直方图;
,则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如右图所示的频率分布直方图; 次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表.
次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表.| 下午开始上课时间 | 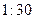 | 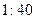 | 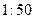 | 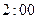 | 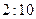 |
| 平均每天午休人数 | 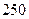 | 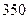 | 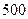 | 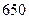 | 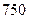 |
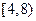 的概率是多少?
的概率是多少?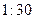 作为横坐标
作为横坐标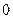 ,然后上课时间每推迟
,然后上课时间每推迟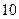 分钟,横坐标
分钟,横坐标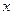 增加2,并以平均每天午休人数作为纵坐标
增加2,并以平均每天午休人数作为纵坐标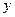 ,试列出
,试列出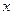 与
与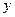 的统计表,并根据表中的数据求平均每天午休人数
的统计表,并根据表中的数据求平均每天午休人数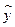 与上课时间
与上课时间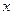 之间的线性回归方程
之间的线性回归方程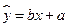 ;
;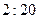 时,家距学校的路程在4里路以下的走读生中约有多少人午休?
时,家距学校的路程在4里路以下的走读生中约有多少人午休?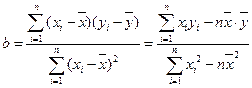 )
)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com