练习册

  • 练习册
  • 试题
    因为＝0. 【查看更多】

     

    题目列表(包括答案和解析)

    因发生意外交通事故，一辆货车上的某种液体泄露到一鱼塘中．为治理污染，根据环保部门的建议，现决定在鱼塘中投放一种可与污染液体发生化学反应的药剂．已知每投放a(1≤a≤4，且a∈R)个单位的药剂，它在水中释放的浓度y(克/升)随着时间(天)变化的函数关系式近似为y＝a·f(x)，其中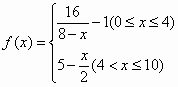．若多次投放，则某一时刻水中的药剂浓度为每次投放的药剂在相应时刻所释放的浓度之和．根据经验，当水中药剂的浓度不低于4(克/升)时，它才能起到有效的治污的作用．

    (Ⅰ)若一次投放4个单位的药剂，则有效治污的时间可达几天？

    (Ⅱ)若因材料紧张，第一次只能投放2个单位的药剂，6天后再投放a个单位的药剂，要使接下来的4天中能够持续有效治污，试求a的最小值(精确到0.1，参考数据：取1.4)．

    查看答案和解析>>

    因发生意外交通事故，一辆货车上的某种液体泄露到一鱼塘中．为治理污染，根据环保部门的建议，现决定在鱼塘中投放一种可与污染液体发生化学反应的药剂．已知每投放a(1≤a≤4，且a∈R)个单位的药剂，它在水中释放的浓度y(克/升)随着时间(天)变化的函数关系式近似为y＝a·f(x)，其中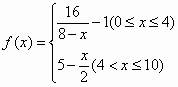．若多次投放，则某一时刻水中的药剂浓度为每次投放的药剂在相应时刻所释放的浓度之和．根据经验，当水中药剂的浓度不低于4(克/升)时，它才能起到有效的治污的作用．

    (Ⅰ)若一次投放4个单位的药剂，则有效治污的时间可达几天？

    (Ⅱ)若因材料紧张，第一次只能投放2个单位的药剂，6天后再投放a个单位的药剂，要使接下来的4天中能够持续有效治污，试求a的最小值(精确到0.1，参考数据：取1.4)．

    查看答案和解析>>

    因发生意外交通事故，一辆货车上的某种液体泄漏到一渔塘中．为了治污，根据环保部门的建议，现决定在渔塘中投放一种可与污染液体发生化学反应的药剂．已知每投放a(1≤a≤4，且a∈R个单位的药剂，它在水中释放的浓度y(克/升)随着时间x(天)变化的函数关系式近似为y＝a·f(x)，其中．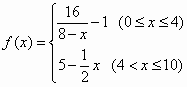

    若多次投放，则某一时刻水中的药剂浓度为每次投放的药剂在相应时刻所释放的浓度之和．根据经验，当水中药剂的浓度不低于4(克/升)时，它才能起到有效治污的作用．

    (1)若一次投放4个单位的药剂，则有效治污时间可达几天？

    (2)若第一次投放2个单位的药剂，6天后再投放a个单位的药剂，要使接下来的4天中能够持续有效治污，试求a的最小值．(精确到0．1，参考数据：取1．4)

    查看答案和解析>>

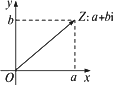
    如下图，设复平面内的点Z表示复数z＝a＋bi，连结，显然向量是由点Z________确定的；反过来，点Z(相对于原点来说)也可以由向量唯一确定．因此，复数集C与复平面内的向量所成的集合也是一一对应的(实数0与零向量对应)，即

    这是复数的另一种几何意义．

    为方便起见，我们常把复数z＝a＋bi说成点Z或说成向量，并且规定，相等的向量表示________复数．

    查看答案和解析>>

    (1)已知sin＋cos＝(0＜＜π)，求tan及sin3－cos3的值．

    (2)在上面的题目中，直接给出了已知sinα±cosα的值，然后利用sinα±cosα与sinα·cosα的关系使题目得到解决．本题也可以变换条件，由于sinα、cosα和差与积有一定的关系，因此，也可以将它们与一元二次方程联系在一起．例如：关于x的方程2x2－(＋1)x＋m＝0的两根为sinα和cosα，且α∈(0，2π)，

    (1)求＋的值；

    (2)求m的值；

    (3)求方程的两根及此时的角α．

    查看答案和解析>>


    同步练习册答案