
题目列表(包括答案和解析)
为了科学地比较考试成绩,有些选拔性考试常常将考试分数转化为标准分Z,转化关系式为Z=![]() ,其中x是某位学生的考试分数,
,其中x是某位学生的考试分数,![]() 是这次考试的平均分,s是这次考试的标准差,Z为这位学生的标准分.转化后的分数可能出现小数或负数,因此,又常将Z分数作线性变换转化为其他分数.例如某次学业选择性考试采用的是T分数,线性变换公式为:T=42Z+58.
是这次考试的平均分,s是这次考试的标准差,Z为这位学生的标准分.转化后的分数可能出现小数或负数,因此,又常将Z分数作线性变换转化为其他分数.例如某次学业选择性考试采用的是T分数,线性变换公式为:T=42Z+58.
已知一组学号(ⅰ)为1-10的学生的某次考试成绩如下:
则学号为1的学生的T分数为________.
为了科学地比较考试成绩,有些选拔性考试常常将考试分数转化为标准分Z,转化关系式为Z=![]() ,其中x是某位学生的考试分数,
,其中x是某位学生的考试分数,![]() 是这次考试的平均分,s是这次考试的学生的标准差,Z为这位学生的标准分.转化后的分数可能出现小数或负数,因此,又常将Z分数作线性变换转化为其他分数.例如某次学业选择性考试采用的是T分数,线性变换公式为T=42Z+58.
是这次考试的平均分,s是这次考试的学生的标准差,Z为这位学生的标准分.转化后的分数可能出现小数或负数,因此,又常将Z分数作线性变换转化为其他分数.例如某次学业选择性考试采用的是T分数,线性变换公式为T=42Z+58.
已知一组学号(i)为1~10的某次考试成绩如下:
则学号为1的T分数为________.
如图,因为AB∥CD,所以∠1=∠2,又因为∠2=∠3,所以∠1=∠3.所用的推理规则为
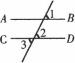
假言推理
关系推理
完全归纳推理
三段论推理
已知函数f(x)=ax3+bx2+cx在x=±1处取得极值,且在x=0处的切线的斜率为-3.
(1)求f(x)的解析式;
(2)若过点A(2,m)可作曲线y=f(x)的三条切线,求实数m的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。第一问,利用函数f(x)=ax3+bx2+cx在x=±1处取得极值,且在x=0处的切线的斜率为-3,得到c=-3 ∴a=1, f(x)=x3-3x
(2)中设切点为(x0,x03-3x0),因为过点A(2,m),所以∴m-(x03-3x0)=(3x02-3)(2-x0)分离参数∴m=-2x03+6x02-6
然后利用g(x)=-2x3+6x2-6函数求导数,判定单调性,从而得到要是有三解,则需要满足-6<m<2
解:(1)f′(x)=3ax2+2bx+c
依题意
又f′(0)=-3
∴c=-3 ∴a=1 ∴f(x)=x3-3x
(2)设切点为(x0,x03-3x0),
∵f′(x)=3x2-3,∴f′(x0)=3x02-3
∴切线方程为y-(x03-3x0)=(3x02-3)(x-x0)
又切线过点A(2,m)
∴m-(x03-3x0)=(3x02-3)(2-x0)
∴m=-2x03+6x02-6
令g(x)=-2x3+6x2-6
则g′(x)=-6x2+12x=-6x(x-2)
由g′(x)=0得x=0或x=2
∴g(x)在(-∞,0)单调递减,(0,2)单调递增,(2,+∞)单调递减.
∴g(x)极小值=g(0)=-6,g(x)极大值=g(2)=2
画出草图知,当-6<m<2时,m=-2x3+6x2-6有三解,
所以m的取值范围是(-6,2).

解析:依题意得f(x)的图象关于直线x=1对称,f(x+1)=-f(x-1),f(x+2)=-f(x),f(x+4)=-f(x+2)=f(x),即函数f(x)是以4为周期的函数.由f(x)在[3,5]上是增函数与f(x)的图象关于直线x=1对称得,f(x)在[-3,-1]上是减函数.又函数f(x)是以4为周期的函数,因此f(x)在[1,3]上是减函数,f(x)在[1,3]上的最大值是f(1),最小值是f(3).
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com