
题目列表(包括答案和解析)
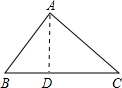 在△ABC中,BC=a,CA=b,AB=c;
在△ABC中,BC=a,CA=b,AB=c;如图1,在△ACD中,AC=2DC,AD=![]() DC .
DC .
(1)求∠C的度数;
(2)如图2,延长CA到E,使AE=CD,延长CD到B,使DB=CE,AB、ED交于点O.求证:∠BOD=45º ;
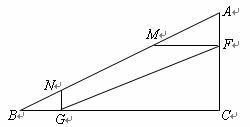
 (3)如图3,点F、G分别是AC、BC上的动点,且S△CFG=S四边形AFGB , 作FM∥BC,GN∥AC,分别交AB于点M、N,线段AM、MN、NB能否始终组成直角三角形?给出你的结论,并说明理由.
(3)如图3,点F、G分别是AC、BC上的动点,且S△CFG=S四边形AFGB , 作FM∥BC,GN∥AC,分别交AB于点M、N,线段AM、MN、NB能否始终组成直角三角形?给出你的结论,并说明理由.

 DC.
DC.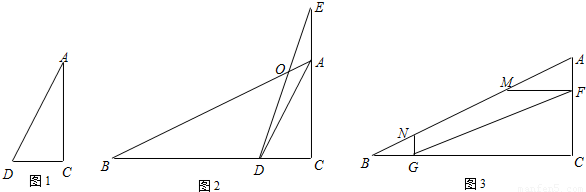
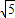 DC.
DC.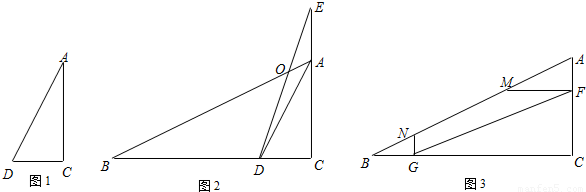
一、阅读理解:
在△ABC中,BC=a,CA=b,AB=c;
(1)若∠C为直角,则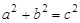 ;
;
(2)若∠C为为锐角,则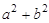 与
与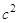 的关系为:
的关系为:
证明:如图过A作AD⊥BC于D,则BD=BC-CD=a-CD
在△ABD中:AD2=AB2-BD2
在△ACD中:AD2=AC2-CD2
AB2-BD2= AC2-CD2
c2-( -CD)2= b2-CD2
-CD)2= b2-CD2
∴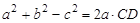
∵ >0,CD>0
>0,CD>0
∴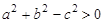 ,所以:
,所以:
(3)若∠C为钝角,试推导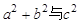 的关系.
的关系.
二、探究问题:在△ABC中,BC=a=3,CA=b=4,AB=c;若△ABC是钝角三角形,求第三边c的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com