
题目列表(包括答案和解析)
设![]() 、
、![]() 是两条不同的直线,
是两条不同的直线,![]() 、
、![]() 是两个不同的平面.考查下列命题,其中正确的命题是( )
是两个不同的平面.考查下列命题,其中正确的命题是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
设 、
、 是两条不同的直线,
是两条不同的直线, 、
、 是两个不同的平面,则下列命题正确的是( )
是两个不同的平面,则下列命题正确的是( )
A.若 则
则 B.若
B.若 则
则
C.若 则
则 D.若
D.若 则
则
设 、
、 是两条不同的直线,
是两条不同的直线, 、
、 是两个不同的平面.下列四个命题中,正确的是(
)
是两个不同的平面.下列四个命题中,正确的是(
)
A. ,
, ,则
,则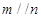
B.
 ,则
,则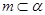
C.
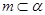 ,
, ,则
,则
D.
 ,
, ,则
,则
设 、
、 是两条不同的直线,
是两条不同的直线, 、
、 是两个不同的平面,则下列正确的个数为:( )
是两个不同的平面,则下列正确的个数为:( )
①若 ,则
,则 ; ②若
; ②若 ,则
,则 ;
;
③若 ,则
,则 或
或 ;④若
;④若 ,则
,则
A.1 B.2 C.3 D.4
设 、
、 是两条不同的直线,
是两条不同的直线, 、
、 是两个不同的平面,给出下列结论:
是两个不同的平面,给出下列结论:
① ∥
∥ ,
,

 ?
? ∥
∥ ;
;
② ∥
∥ ,
, ∥
∥ ,
,

 ?
? ∥
∥ ;
;
③

 =
= ,
, ∥
∥ ,
, ∥
∥ ?
? ∥
∥ ;
;
④ ∥
∥ ,
,

 ?
? ∥
∥ .
.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
三、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
D
A
B
B
D
B
D
A
B
C
B
四、填空题
13.2 14. 31 15. .files/image183.gif) 16. 2.
16. 2.
三、解答题
17.17.解:(Ⅰ).files/image185.gif)
.files/image187.gif)
.files/image189.gif) .
.
.files/image191.gif) 的最小正周期
的最小正周期.files/image193.gif) .
.
(Ⅱ)由.files/image195.gif) 解得
解得
.files/image197.gif)
∴ .files/image095.gif) 的单调递增区间为
的单调递增区间为.files/image199.gif) 。
。
18.(Ⅰ)解:设“从甲盒内取出的2个球均为红球”为事件.files/image201.gif) ,“从乙盒内取出的2个球均为红球”为事件
,“从乙盒内取出的2个球均为红球”为事件.files/image203.gif) .由于事件
.由于事件.files/image205.gif) 相互独立,且
相互独立,且
.files/image207.gif) ,
,.files/image209.gif) ,
,
故取出的4个球均为红球的概率是
.files/image211.gif) .
.
(Ⅱ)解:设“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个红球为黑球”为事件.files/image213.gif) ,“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件
,“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件.files/image215.gif) .由于事件
.由于事件.files/image217.gif) 互斥,且
互斥,且
.files/image219.gif) ,
,.files/image221.gif) .
.
故取出的4个红球中恰有4个红球的概率为
.files/image223.gif) .
.
19.(Ⅰ)取DC的中点E.
∵ABCD是边长为.files/image045.gif) 的菱形,
的菱形,.files/image135.gif) ,∴BE⊥CD.
,∴BE⊥CD.
∵.files/image137.gif) 平面
平面.files/image139.gif) , BE
, BE.files/image037.gif) 平面
平面.files/image139.gif) ,∴
,∴.files/image137.gif) BE.
BE.
∴BE⊥平面PDC.∠BPE为求直线PB与平面PDC所成的角.
∵BE=.files/image226.gif) ,PE=
,PE=.files/image228.gif) ,∴
,∴.files/image230.gif) =
=.files/image232.gif) =
=.files/image234.gif) .
.
(Ⅱ)连接AC、BD交于点O,因为ABCD是菱形,所以AO⊥BD.
∵.files/image137.gif) 平面
平面.files/image139.gif) , AO
, AO.files/image037.gif) 平面
平面.files/image139.gif) ,
,
∴.files/image236.gif) PD. ∴AO⊥平面PDB.
PD. ∴AO⊥平面PDB.
作OF⊥PB于F,连接AF,则AF⊥PB.
故∠AFO就是二面角A-PB-D的平面角.
∵AO=.files/image226.gif) ,OF=
,OF=.files/image239.gif) ,∴
,∴.files/image241.gif) =
=.files/image243.gif) .
.
20.解:(1)令.files/image245.gif) 得所求增区间为
得所求增区间为.files/image247.gif) ,
,.files/image249.gif) 。
。
(2)要使当.files/image250.gif) 时
时.files/image251.gif) 恒成立,只要当
恒成立,只要当.files/image250.gif) 时
时 .files/image253.gif) 。
。
由(1)知
当.files/image255.gif) 时,
时,.files/image256.gif) 是增函数,
是增函数,.files/image258.gif) ;
;
当.files/image260.gif) 时,
时,.files/image256.gif) 是减函数,
是减函数,.files/image262.gif) ;
;
当.files/image264.gif) 时,
时,.files/image256.gif) 是增函数,
是增函数,.files/image266.gif)
由.files/image268.gif) ,因此
,因此.files/image266.gif) 故
故.files/image270.gif) 。
。
21. 证明:由.files/image272.gif) 是关于x的方程
是关于x的方程.files/image274.gif) 的两根得
的两根得
.files/image276.gif) 。
。
.files/image278.gif)
.files/image280.gif) ,
,.files/image282.gif)
.files/image284.gif) 是等差数列。
是等差数列。
(2)由(1)知.files/image286.gif)
.files/image288.gif)
.files/image290.gif) 。
。
.files/image292.gif) 。
。
又.files/image294.gif) 符合上式,
符合上式,.files/image296.gif) 。
。
(3).files/image298.gif) ①
①
.files/image300.gif) ②
②
①―②得 .files/image302.gif) 。
。
.files/image304.gif)
.files/image306.gif)
.files/image308.gif) 。
。
22. (1)∵.files/image310.gif)
∴.files/image312.gif)
令.files/image314.gif) ,∴
,∴.files/image316.gif) 或
或.files/image318.gif)
若.files/image320.gif) ,
,
在点.files/image316.gif) 附近,当
附近,当.files/image322.gif) 时,
时,.files/image324.gif) ;当
;当.files/image326.gif) 时,
时,.files/image328.gif)
∴.files/image316.gif) 是函数
是函数.files/image173.gif) 的极小值点,极小值为
的极小值点,极小值为.files/image330.gif) ;
;
在点.files/image318.gif) 附近,当
附近,当.files/image332.gif) 时,
时,.files/image328.gif) ;当
;当.files/image335.gif) 时,
时,.files/image324.gif)
∴.files/image318.gif) 是函数
是函数.files/image173.gif) 的极大值点,极大值为
的极大值点,极大值为.files/image338.gif)
若.files/image340.gif) ,易知,
,易知,
.files/image316.gif) 是函数
是函数.files/image173.gif) 的极大值点,极大值为
的极大值点,极大值为.files/image330.gif) ;
;
.files/image318.gif) 是函数
是函数.files/image173.gif) 的极小值点,极小值为
的极小值点,极小值为.files/image338.gif)
(2)若在.files/image175.gif) 上至少存在一点
上至少存在一点.files/image177.gif) 使得
使得.files/image179.gif) 成立,
成立,
则.files/image342.gif) 在
在.files/image175.gif) 上至少存在一解,即
上至少存在一解,即.files/image344.gif) 在
在.files/image175.gif) 上至少存在一解
上至少存在一解
由(1)知,
当.files/image340.gif) 时,函数
时,函数.files/image173.gif) 在区间
在区间.files/image175.gif) 上递增,且极小值为
上递增,且极小值为.files/image346.gif)
∴此时.files/image344.gif) 在
在.files/image175.gif) 上至少存在一解;
上至少存在一解;
当.files/image320.gif) 时,函数
时,函数.files/image173.gif) 在区间
在区间.files/image349.gif) 上递增,在
上递增,在.files/image351.gif) 上递减,
上递减,
∴要满足条件应有函数.files/image173.gif) 的极大值
的极大值.files/image353.gif) ,即
,即.files/image355.gif)
综上,实数.files/image045.gif) 的取值范围为
的取值范围为.files/image340.gif) 或
或.files/image355.gif) 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com