
题目列表(包括答案和解析)
在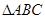 中,下列命题中正确的有:_____;
中,下列命题中正确的有:_____;
①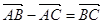 ;
②若
;
②若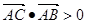 ,则
,则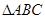 为锐角三角形;
为锐角三角形;
③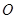 是
是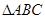 所在平面内一定点,动点
所在平面内一定点,动点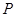 满足
满足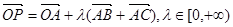 ,则动点
,则动点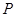 一定过
一定过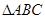 的重心;
的重心;
④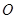 是
是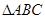 内一定点,且
内一定点,且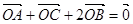 ,则
,则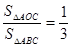 ;
;
⑤若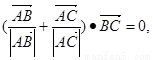 且
且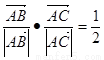 ,则
,则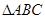 为等边三角形。
为等边三角形。
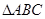 中,下列命题中正确的有:_____;
中,下列命题中正确的有:_____;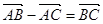 ; ②若
; ②若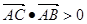 ,则
,则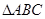 为锐角三角形;
为锐角三角形;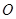 是
是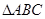 所在平面内一定点,动点
所在平面内一定点,动点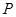 满足
满足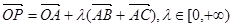 ,则动点
,则动点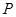 一定过
一定过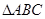 的重心;
的重心;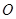 是
是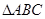 内一定点,且
内一定点,且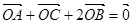 ,则
,则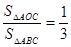 ;
;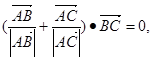 且
且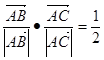 ,则
,则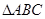 为等边三角形。
为等边三角形。在空间中有以下四个命题:
①垂直于同一条直线的两条直线互相平行;
②垂直于同一个平面的两个平面互相平行;
③若平面α内任意一条直线均平行于平面β,则平面α∥平面β;
④若点P到三角形三个顶点的距离相等,则点P在该三角形所在平面上的射影是该三角形的外心.
其中正确命题的序号为
A.①②
B.③④
C.②③
D.②④
| AB |
| AC |
| BC |
| AC |
| AB |
| OP |
| 0A |
| AB |
| AC |
| OA |
| OC |
| OB |
| 0 |
| S△AOC |
| S△ABC |
| 1 |
| 3 |
| ||
丨
|
| ||
丨
|
| BC |
| ||
丨
|
| ||
丨
|
| 1 |
| 2 |
如图,在直角梯形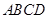 中,
中,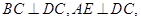
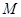 、
、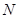 分别是
分别是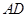 、
、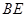 的中点,将三角形
的中点,将三角形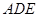 沿
沿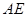 折起。下列说法正确的是 .(填上所有正确的序号)
折起。下列说法正确的是 .(填上所有正确的序号)
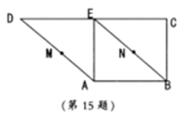
①不论 折至何位置(不在平面
折至何位置(不在平面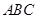 内)都有
内)都有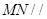 平面
平面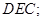
②不论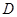 折至何位置都有
折至何位置都有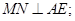
③不论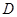 折至何位置(不在平面
折至何位置(不在平面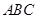 内)都有
内)都有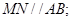
④在折起过程中,一定存在某个位置,使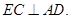
一、选择题(本大题共8小题,每小题5分,共40分)
1.D 2.A 3.B 4.C 5.D 6.B 7.C 8. A
二、填空题(本大题共6小题,每小题5分,共30分)
9.数学文科.files/image252.gif) 点
10.
点
10.数学文科.files/image254.gif) 11. 6 , 60
11. 6 , 60
12.数学文科.files/image256.gif) 13.
13.数学文科.files/image258.gif) 14.
14. 数学文科.files/image260.gif) ,
,数学文科.files/image262.gif)
注:两个空的填空题第一个空填对得2分,第二个空填对得3分.
三、解答题(本大题共6小题,共80分)
15. (本小题满分13分)
解:(Ⅰ)设等比数列数学文科.files/image012.gif) 的公比为
的公比为数学文科.files/image010.gif) ,依题意有
,依题意有数学文科.files/image266.gif) , (1)
, (1)
又数学文科.files/image158.gif) ,将(1)代入得
,将(1)代入得数学文科.files/image269.gif) .所以
.所以数学文科.files/image271.gif) . ……………3分
. ……………3分
于是有数学文科.files/image273.gif) ………………4分
………………4分
解得数学文科.files/image275.gif) 或
或数学文科.files/image277.gif) ………………6分
………………6分
又数学文科.files/image012.gif) 是递增的,故
是递增的,故数学文科.files/image279.gif) . ………………7分
. ………………7分
所以数学文科.files/image281.gif) .
………………9分
.
………………9分
(Ⅱ)数学文科.files/image283.gif) .
…………………11分
.
…………………11分
故数学文科.files/image285.gif) .
………………13分
.
………………13分
16.(本小题满分13分)
解:(Ⅰ)在△数学文科.files/image170.gif) 中,由
中,由数学文科.files/image288.gif) 得
得数学文科.files/image290.gif) .
.
所以数学文科.files/image292.gif) .
…………………5分
.
…………………5分
(Ⅱ)由数学文科.files/image178.gif) 得
得数学文科.files/image295.gif) . ………………………………….9分
. ………………………………….9分
又数学文科.files/image297.gif) ,
,数学文科.files/image299.gif)
数学文科.files/image301.gif) =
=数学文科.files/image303.gif) ;
………………………11分
;
………………………11分
于是有数学文科.files/image305.gif) ,解得
,解得数学文科.files/image307.gif) .
……………………………13分
.
……………………………13分
数学文科.files/image308.gif) |
17.(本小题满分14分)
解法一:(Ⅰ)∵正方形数学文科.files/image310.gif) ,∴
,∴数学文科.files/image312.gif)
又二面角数学文科.files/image314.gif) 是直二面角,
是直二面角,
∴数学文科.files/image316.gif) ⊥平面
⊥平面数学文科.files/image187.gif) .
.
∵数学文科.files/image319.gif)
数学文科.files/image321.gif) 平面
平面数学文科.files/image187.gif) ,
,
∴数学文科.files/image316.gif) ⊥
⊥数学文科.files/image319.gif) .
.
又数学文科.files/image326.gif) ,
,数学文科.files/image328.gif) ,
,数学文科.files/image187.gif) 是矩形,
是矩形,数学文科.files/image133.gif) 是
是数学文科.files/image194.gif) 的中点,
的中点,
∴数学文科.files/image333.gif) =
=数学文科.files/image335.gif) ,
,数学文科.files/image337.gif) ,
,数学文科.files/image339.gif) =
=数学文科.files/image341.gif) ,
,
∴数学文科.files/image319.gif) ⊥
⊥数学文科.files/image344.gif) 又
又数学文科.files/image316.gif)
数学文科.files/image347.gif) =
=数学文科.files/image125.gif) ,
,
∴数学文科.files/image319.gif) ⊥平面
⊥平面数学文科.files/image351.gif) ,
,
而数学文科.files/image319.gif)
数学文科.files/image321.gif) 平面
平面数学文科.files/image354.gif) ,故平面
,故平面数学文科.files/image354.gif) ⊥平面
⊥平面数学文科.files/image351.gif) .
……………………5分
.
……………………5分
(Ⅱ)如图,由(Ⅰ)知平面数学文科.files/image354.gif) ⊥平面
⊥平面数学文科.files/image351.gif) ,且交于
,且交于数学文科.files/image360.gif) ,在平面
,在平面数学文科.files/image351.gif) 内作
内作数学文科.files/image363.gif) ⊥
⊥数学文科.files/image360.gif) ,垂足为
,垂足为数学文科.files/image366.gif) ,则
,则数学文科.files/image363.gif) ⊥平面
⊥平面数学文科.files/image354.gif) .
.
∴∠数学文科.files/image370.gif) 是
是数学文科.files/image372.gif) 与平面
与平面数学文科.files/image354.gif) 所成的角.
所成的角.
∴在Rt△数学文科.files/image375.gif) 中,
中,数学文科.files/image372.gif) =
=数学文科.files/image378.gif) .
.
数学文科.files/image380.gif) .
.
即数学文科.files/image372.gif) 与平面
与平面数学文科.files/image354.gif) 所成的角为
所成的角为数学文科.files/image382.gif) .
………………………9分
.
………………………9分
(Ⅲ)由(Ⅱ),数学文科.files/image363.gif) ⊥平面
⊥平面数学文科.files/image354.gif) .作
.作数学文科.files/image386.gif) ⊥
⊥数学文科.files/image388.gif) ,垂足为
,垂足为数学文科.files/image390.gif) ,连结
,连结数学文科.files/image392.gif) ,则
,则数学文科.files/image392.gif) ⊥
⊥数学文科.files/image388.gif) ,
,
∴∠数学文科.files/image396.gif) 为二面角
为二面角数学文科.files/image398.gif) 的平面角.
…………….11分
的平面角.
…………….11分
∵在Rt△数学文科.files/image170.gif) 中,
中,数学文科.files/image386.gif) =
=数学文科.files/image402.gif)
数学文科.files/image185.gif) ,在Rt△
,在Rt△数学文科.files/image375.gif) 中,
中,数学文科.files/image406.gif) .
.
∴在Rt△数学文科.files/image396.gif) 中,
中,数学文科.files/image409.gif)
数学文科.files/image410.gif) 即二面角
即二面角数学文科.files/image398.gif) 的大小为arcsin
的大小为arcsin数学文科.files/image413.gif) . ………………………………14分
. ………………………………14分
解法二:
如图,以数学文科.files/image252.gif) 为原点建立直角坐标系
为原点建立直角坐标系数学文科.files/image416.gif) ,
,
则数学文科.files/image252.gif) (0,0,0),
(0,0,0),数学文科.files/image125.gif) (0,2
(0,2数学文科.files/image185.gif) ,0),
,0),
数学文科.files/image218.gif) (0,2
(0,2数学文科.files/image185.gif) ,2
,2数学文科.files/image185.gif) ),
),数学文科.files/image133.gif) (
(数学文科.files/image185.gif) ,
,数学文科.files/image185.gif) ,0),
,0),
数学文科.files/image129.gif) (
(数学文科.files/image185.gif) ,0,0).
,0,0).
(Ⅰ)数学文科.files/image429.gif) =(
=(数学文科.files/image185.gif) ,
,数学文科.files/image185.gif) ,0),
,0),数学文科.files/image433.gif) =(
=(数学文科.files/image185.gif) ,
,数学文科.files/image436.gif) ,0),
,0),
数学文科.files/image438.gif) =(0,0,2
=(0,0,2数学文科.files/image185.gif) ),
),
∴数学文科.files/image429.gif) ?
?数学文科.files/image433.gif) =(
=(数学文科.files/image185.gif) ,
,数学文科.files/image185.gif) ,0)?(
,0)?(数学文科.files/image185.gif) ,
,数学文科.files/image436.gif) ,0)=0,
,0)=0,
数学文科.files/image429.gif) ?
?数学文科.files/image438.gif) =(
=(数学文科.files/image185.gif) ,
,数学文科.files/image185.gif) ,0)?(0,0,2
,0)?(0,0,2数学文科.files/image185.gif) )= 0.
)= 0.
∴数学文科.files/image319.gif) ⊥
⊥数学文科.files/image372.gif) ,
,数学文科.files/image319.gif) ⊥
⊥数学文科.files/image445.gif) ,
,
∴数学文科.files/image319.gif) ⊥平面
⊥平面数学文科.files/image351.gif) ,又
,又数学文科.files/image319.gif)
数学文科.files/image321.gif) 平面
平面数学文科.files/image354.gif) ,故平面
,故平面数学文科.files/image451.gif) ⊥平面
⊥平面数学文科.files/image351.gif) . ……5分
. ……5分
(Ⅱ)设数学文科.files/image200.gif) 与平面
与平面数学文科.files/image354.gif) 所成角为
所成角为数学文科.files/image456.gif) .
.
由题意可得数学文科.files/image429.gif) =(
=(数学文科.files/image185.gif) ,
,数学文科.files/image185.gif) ,0),
,0),数学文科.files/image460.gif) =(0,2
=(0,2数学文科.files/image185.gif) ,2
,2 数学文科.files/image185.gif) ),
),数学文科.files/image433.gif) =(
=(数学文科.files/image185.gif) ,
,数学文科.files/image436.gif) ,0).
,0).
设平面数学文科.files/image354.gif) 的一个法向量为
的一个法向量为数学文科.files/image467.gif) =(
=(数学文科.files/image042.gif) ,
,数学文科.files/image470.gif) ,1),
,1),
由数学文科.files/image472.gif) .
.
数学文科.files/image474.gif) .
.
∴数学文科.files/image200.gif) 与平面
与平面数学文科.files/image354.gif) 所成角的大小为
所成角的大小为数学文科.files/image477.gif) .
……………..9分
.
……………..9分
(Ⅲ)因数学文科.files/image467.gif) =(1,-1,1)是平面
=(1,-1,1)是平面数学文科.files/image354.gif) 的一个法向量,
的一个法向量,
又数学文科.files/image481.gif) ⊥平面
⊥平面数学文科.files/image310.gif) ,平面
,平面数学文科.files/image310.gif) 的一个法向量
的一个法向量数学文科.files/image485.gif) =(
=(数学文科.files/image185.gif) ,0,0),
,0,0),
∴设数学文科.files/image467.gif) 与
与数学文科.files/image485.gif) 的夹角为
的夹角为数学文科.files/image014.gif) ,得
,得数学文科.files/image489.gif) ,
,
∴二面角数学文科.files/image398.gif) 的大小为
的大小为数学文科.files/image492.gif)
数学文科.files/image494.gif) .
………………………………14分
.
………………………………14分
18. (本小题满分13分)
解: (Ⅰ)由已知甲射击击中8环的概率为0.2,乙射击击中9环的概率为0.4,则所求事件的概率
数学文科.files/image496.gif) .
………………4分
.
………………4分
(Ⅱ) 设事件数学文科.files/image252.gif) 表示“甲运动员射击一次,击中9环以上(含9环)”, 记“乙运动员射击1次,击中9环以上(含9环)”为事件
表示“甲运动员射击一次,击中9环以上(含9环)”, 记“乙运动员射击1次,击中9环以上(含9环)”为事件数学文科.files/image125.gif) ,则
,则
数学文科.files/image500.gif) .
………………………6分
.
………………………6分
数学文科.files/image502.gif) .
………………………8分
.
………………………8分
“甲、乙两运动员各自射击两次,这4次射击中恰有3次击中9环以上(含9环)”包含甲击中2次、乙击中1次,与甲击中1次、乙击中2次两个事件,显然,这两个事件互斥.
甲击中2次、乙击中1次的概率为
数学文科.files/image504.gif) ;
……………………..10分
;
……………………..10分
甲击中1次、乙击中2次的概率为
数学文科.files/image506.gif) .
…………………12分
.
…………………12分
所以所求概率为数学文科.files/image508.gif) .
.
答: 甲、乙两运动员各自射击两次,这4次射击中恰有3次击中9环以上的概率为数学文科.files/image510.gif) . ……….13分
. ……….13分
19.(本小题满分14分)
解: (Ⅰ) 由已知数学文科.files/image512.gif) , 又圆心
, 又圆心数学文科.files/image218.gif)
数学文科.files/image515.gif) ,则
,则数学文科.files/image517.gif) .故
.故数学文科.files/image519.gif) .
.
所以直线数学文科.files/image214.gif) 与
与数学文科.files/image044.gif) 垂直.
………………………3分
垂直.
………………………3分
(Ⅱ) 当直线数学文科.files/image214.gif) 与
与数学文科.files/image042.gif) 轴垂直时,易知
轴垂直时,易知数学文科.files/image525.gif) 符合题意; ………………4分
符合题意; ………………4分
当直线与数学文科.files/image042.gif) 轴不垂直时,设直线
轴不垂直时,设直线数学文科.files/image214.gif) 的方程为
的方程为数学文科.files/image529.gif) . …………5分
. …………5分
由于数学文科.files/image531.gif) ,所以
,所以数学文科.files/image533.gif)
由数学文科.files/image535.gif) ,解得
,解得数学文科.files/image537.gif) .
………………7分
.
………………7分
故直线数学文科.files/image214.gif) 的方程为
的方程为数学文科.files/image525.gif) 或
或数学文科.files/image541.gif) .
………………8分
.
………………8分
(Ⅲ)当数学文科.files/image214.gif) 与
与数学文科.files/image042.gif) 轴垂直时,易得
轴垂直时,易得数学文科.files/image545.gif) ,
,数学文科.files/image547.gif) ,又
,又数学文科.files/image212.gif) 则
则数学文科.files/image550.gif)
数学文科.files/image552.gif) ,故
,故数学文科.files/image554.gif) .
………………10分
.
………………10分
当数学文科.files/image214.gif) 的斜率存在时,设直线
的斜率存在时,设直线数学文科.files/image214.gif) 的方程为
的方程为数学文科.files/image529.gif) ,代入圆的方程得
,代入圆的方程得
数学文科.files/image559.gif) .则
.则数学文科.files/image561.gif)
数学文科.files/image563.gif) ,即
,即数学文科.files/image565.gif) ,
,
数学文科.files/image567.gif)
数学文科.files/image569.gif) .又由
.又由数学文科.files/image571.gif) 得
得数学文科.files/image573.gif) ,
,
则数学文科.files/image575.gif) .
.
故数学文科.files/image577.gif)
数学文科.files/image579.gif) .
.
综上,数学文科.files/image239.gif) 的值与直线
的值与直线数学文科.files/image214.gif) 的斜率无关,且
的斜率无关,且数学文科.files/image554.gif) . …………14分
. …………14分
另解一:连结数学文科.files/image584.gif) ,延长交
,延长交数学文科.files/image044.gif) 于点
于点数学文科.files/image587.gif) ,由(Ⅰ)知
,由(Ⅰ)知数学文科.files/image589.gif) .又
.又数学文科.files/image591.gif) 于
于数学文科.files/image222.gif) ,
,
故△数学文科.files/image594.gif) ∽△
∽△数学文科.files/image596.gif) .于是有
.于是有数学文科.files/image598.gif) .
.
由数学文科.files/image600.gif) 得
得数学文科.files/image602.gif)
故数学文科.files/image604.gif)
数学文科.files/image606.gif) ………………………14分
………………………14分
另解二:连结数学文科.files/image584.gif) 并延长交直线
并延长交直线数学文科.files/image044.gif) 于点
于点数学文科.files/image125.gif) ,连结
,连结数学文科.files/image611.gif) 由(Ⅰ)知
由(Ⅰ)知数学文科.files/image613.gif) 又
又数学文科.files/image591.gif) ,
,
所以四点
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com