题目列表(包括答案和解析)
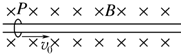如图所示，质量为m、带电荷量为+q的P环套在固定的水平长直绝缘杆上（杆表面不光滑），整个装置处在垂直于杆的水平匀强磁场中，磁感应强度大小为B．现给环一向右的初速度v0，则下列情况可能发生的是（ ）
如图所示，质量为m、带电荷量为+q的粒子，从两平行电极板正中央垂直电场线和磁感线以速度v飞入．已知两极间距为d，磁感应强度为B，这时粒子恰能沿直线穿过电场和磁场区域．今将磁感应强度增大到某值，则粒子将落到极板上．已知粒子重力不计，则粒子落到极板上时的动能为多少？
如图所示，质量为m、带电荷量为q的粒子，以初速度v0沿偏转电场的中心线射入，极板间距为d，极板长为l，偏转电场所加电压为U，射出后打在距极板右端L远处的竖直荧光屏上，求打在荧光屏上的亮斑距荧光屏中心（荧光屏中心与偏转电场两极板的中心线在同一水平直线上）的距离y′．
A.小球在未受冲量前悬线张力大小为mg
B.小球做匀速圆周运动时悬线所受张力保持不变
C.U=mgd/q
D.板间场强E=mg/q
（1）如果在某方向加上一定大小的匀强电场后，能保证粒子仍沿v0方向做直线运动，试求所加匀强电场的最小值;
（2）若加上大小一定、方向水平向左的匀强电场，仍能保证粒子沿v0方向做直线运动，并经过一段时间后又返回O点，求粒子回到O点时的速率.
一
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
A
B
BD
AD
CD
BD
BD
ABD
B
AC
二
13．（1）将玻璃板放在盘上，用笔画出油膜的形状(2分) 
(3分)
（2）（1）
14．
（6分）
15题．（共8分）
解：该队员先在t1=1s时间内以a1匀加速下滑．
然后在t2=1.5s时间内以a2匀减速下滑．
第1s由牛顿第二定律得：mg－F1=ma1
所以a1=
=
最大速度vm=a1t1
代入数据解得：vm=
后1.5s由牛顿第二定律得：F2－mg=ma2
a2=
=
队员落地时的速度v=vm－a2t2
代入数据解得：v=
16（8分）题将运动员看成质量为m的质点，从高
处下落，刚接触网时的速度的大小
①
（2分）
弹跳后到达的高度为
，刚离网时的速度的大小
②
（2分）
接触过程中运动员受到向下的重力mg和网向上的弹力F。选取竖直向上为正方向，由动量定理，得
③
（3分）
由以上三式解得
代入数值得 
（1分）
17．（12分）
(1)mv0=2mvA…………………………（3分） vA =
v0……………………（1分）
(2)qE=2mv
E= 
……………………………………………………………（1分）
E的方向是: 竖直向上………………………………………………（1分）
(3)在AB过程中应用动能定理有： qE?2r-2mg?2r=EkB-?2mv2共…………………（3分）
∴EkB=
mv20-4mgr………………………………………………………（1分）
18．（12分）参考解答：
（1）开始时弹簧形变量为
，
由平衡条件：
①…………… （1分）
设当A刚离开档板时弹簧的形变量为
：
由：
②…………………………（1分）
故C下降的最大距离为：
③…………………………（2分）
由①～③式可解得
④………………………… （2分）
（2）由能量守恒定律可知：C下落h过程中，C重力势能的的减少量等于B的电势能的增量和弹簧弹性势能的增量以及系统动能的增量之和
当C的质量为M时：
⑤………………（2分）
当C的质量为
⑥ ……………（2分）
由④～⑥式可解得A刚离开P时B的速度为：
⑦…………………………（2分）
19题：（14分）
（1）m1与m2碰撞过程满足
mv0=mv1+2mv2 （1分）
mv02=mv12+2mv22
（1分）
得v1＝-
（负号表示逆时针返回），v2＝-
（2分）
（2）因为m2=m3=＝v2
（2分）
所以m3以的速度顺时针由C向A运动，与m1逆时针返回，
因为v2=v3=2v1， 
+
=2
所以m3和m1同时到达A点并进行碰撞。 （2分）
（3）m3和m1碰撞过程满足
-m=m v1′+
)2+m()2=m v1′2+
解之得v1′＝v0，v3′＝0（另一解v1′＝-，v3′＝，这表示互相穿过去，不可能，所以舍去）即碰后m3停止，m1以v0再次顺时针运动。
（4分）
m1和m2第一次相碰后，返回A点的时间t1=
=
m1和m3在A处碰后，m1以v0返回到C的时间t2=
＝
从m1和m3在第一次相碰，到m1和m2第二次相碰经历的总时间
t= t1+ t2=
（2分）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com