
题目列表(包括答案和解析)
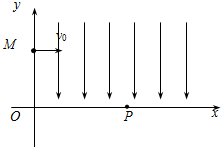 如图,在平面直角坐标系xoy内,第Ⅰ象限存在沿y轴负方向的匀强电场;第Ⅰ、Ⅳ象限某一区域内存在垂直于坐标平面向外的圆形匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子(不计粒子重力),从M(0,
如图,在平面直角坐标系xoy内,第Ⅰ象限存在沿y轴负方向的匀强电场;第Ⅰ、Ⅳ象限某一区域内存在垂直于坐标平面向外的圆形匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子(不计粒子重力),从M(0,| 3 |
 如图,在平面直角坐标系xOy内,第Ⅰ象限存在沿y轴负方向的匀强电场,第Ⅳ象限以ON为直径的半圆形区域内,存在垂直于坐标平面向外的匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子,从y轴正半轴上y=h处的M点,以速度v0垂直于y轴射入电场,经x轴上x=2h处的P点进入磁场,最后以垂直于y轴的方向射出磁场.不计粒子重力.则电场强度大小E=
如图,在平面直角坐标系xOy内,第Ⅰ象限存在沿y轴负方向的匀强电场,第Ⅳ象限以ON为直径的半圆形区域内,存在垂直于坐标平面向外的匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子,从y轴正半轴上y=h处的M点,以速度v0垂直于y轴射入电场,经x轴上x=2h处的P点进入磁场,最后以垂直于y轴的方向射出磁场.不计粒子重力.则电场强度大小E=| mv02 |
| 2qh |
| mv02 |
| 2qh |
| 2h |
| v0 |
| 3πm |
| 4Bq |
| 2h |
| v0 |
| 3πm |
| 4Bq |
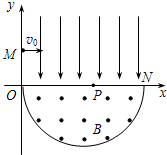 如图,在平面直角坐标系xOy内,第Ⅰ象限存在沿y轴负方向的匀强电场,第Ⅳ象限以ON为直径的半圆形区域内,存在垂直于坐标平面向外的匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子,从y轴上y=h处的M点,以速度v0垂直于y轴射入电场,经x轴上x=2h处的P点进入磁场,最后以垂直于y轴的方向射出磁场.不计粒子重力.求
如图,在平面直角坐标系xOy内,第Ⅰ象限存在沿y轴负方向的匀强电场,第Ⅳ象限以ON为直径的半圆形区域内,存在垂直于坐标平面向外的匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子,从y轴上y=h处的M点,以速度v0垂直于y轴射入电场,经x轴上x=2h处的P点进入磁场,最后以垂直于y轴的方向射出磁场.不计粒子重力.求()如图,在平面直角坐标系xOy内,第Ⅰ象限存在沿y轴负方向的匀强电场,第Ⅳ象限以ON为直径的半圆形区域内,存在垂直于坐标平面向外的匀强磁场,磁感应强度为B。一质量为m、电荷量为q的带正电的粒子,从y轴正半轴上y = h处的M点,以速度v0垂直于y轴射入电场,经x轴上x = 2h处的P点进入磁场,最后以垂直于y轴的方向射出磁场。不计粒子重力。求
(1)电场强度大小E ;
(2)粒子在磁场中运动的轨道半径r;
(3)粒子从进入电场到离开磁场经历的总时间t。
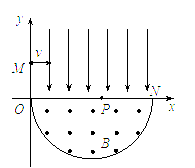
如图,在平面直角坐标系xOy内,第1象限存在沿y轴负方向的匀强电场,第IV象限以ON为直径的半圆形区域内,存在垂直于坐标平面向外的匀强磁场,磁感应强度为B。一质量为m、电荷量为q的带正电的粒子,从y轴正半轴上y=h处的M点,以速度v0垂直于y轴射入电场,经x轴上x=2h处的P点进入磁场,最后以垂直于y轴的方向射出磁场。不计粒子重力。求
(1)电场强度大小E;
(2)粒子在磁场中运动的轨道半径r;
(3)粒子从进入电场到离开磁场经历的总时间t。
一、选择题(全部选对得4分,选对但不全的得2分,有选错的得0分。共16小题,满分64分)
题号
1
2
3
4
5
6
7
8
答案
C
BCD
AD
D
BCD
AC
D
AD
题号
9
10
11
12
13
14
15
16
答案
C
D
BD
BC
C
AD
ABD
D
二.
17.(9分)
(1)根据法拉第电磁感应定律 (2分)
(2分)
求出 E = 1.2(V) (1分)
(2)根据全电路欧姆定律
 (2分)
(2分)
根据  = 5.76×10-2(W) (1分)
= 5.76×10-2(W) (1分)
)
(3)S断开后,流经R2的电量即为S闭合时C板上所带的电量Q
电容器两端的电压 U = IR2=0.6(V) (1分)
流经R2的电量 Q = CU = 1.8×10-5(C) (2分)
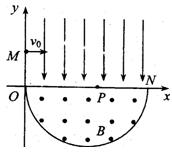
 18.(10分)粒子的运动轨迹如右图所示
18.(10分)粒子的运动轨迹如右图所示
(1)设粒子在电场中运动的时间为t1
x、y方向 2h = v0t1  (2分)
(2分)
根据牛顿第二定律 Eq = ma (1分)
求出
 (1分)
(1分)
(2)根据动能定理  (1分)
(1分)
设粒子进入磁场时速度为v,根据 (1分)
(1分)
求出
 (1分)
(1分)
(3)粒子在磁场中运动的周期  (1分)
(1分)
设粒子在磁场中运动的时间为t2  (1分)
(1分)
求出  (1分)
(1分)
19.(3+3+4=10分)(1) ;(2)
;(2) ;(3)下表面
;(3)下表面 
20.(4+3=7分)
(1)磁场和电场方向与yOz平面平行,与-y方向成53°斜向下;(2)0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com