
题目列表(包括答案和解析)
(满分12分)直线l 与抛物线y2 = 4x 交于两点A、B,O 为原点,且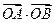 = -4.
= -4.
(I) 求证:直线l 恒过一定点;
(II) 若 4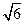 ≤| AB | ≤
≤| AB | ≤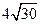 ,求直线l 的
,求直线l 的 斜率k 的取值范围;
斜率k 的取值范围;
(Ⅲ) 设抛物线的焦点为F,∠AFB = θ,试问θ 角 能否
能否 等于120°?若能,求出相应的直线l 的方程;若不能,请说明理由.
等于120°?若能,求出相应的直线l 的方程;若不能,请说明理由.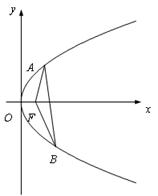
(本小题满分12分)
如图,在边长为4的菱形 中,
中, .点
.点 分别在边
分别在边 上,点
上,点 与点
与点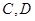 不重合,
不重合, ,
, .沿
.沿 将
将 翻折到
翻折到 的位置,使平面
的位置,使平面 ⊥平面
⊥平面 .
.

(1)求证: ⊥平面
⊥平面 ;
;
(2)当 取得最小值时,请解答以下问题:
取得最小值时,请解答以下问题:
(i)求四棱锥 的体积;
的体积;
(ii)若点 满足
满足 =
=
 (
( ),试探究:直线
),试探究:直线 与平面
与平面 所成角的大小是否一定大于
所成角的大小是否一定大于 ?并说明理由.
?并说明理由.
(本小题满分12分)
如图,在三棱锥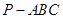 中,
中,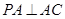 ,
,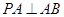 ,
,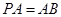 ,
,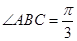 ,
,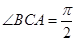 , 点
, 点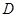 ,
,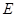 分别在棱
分别在棱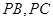 上,且
上,且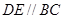 ,
,
(I)求证: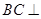 平面
平面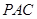 ;
;
(II)当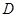 为
为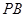 的中点时,求
的中点时,求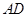 与平面
与平面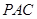 所成的角的大小;
所成的角的大小;
(III)是否存在点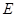 使得二面角
使得二面角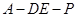 为直二面角?并说明理由.
为直二面角?并说明理由.
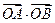 = -4.
= -4.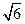 ≤| AB | ≤
≤| AB | ≤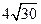 ,求直线l 的
,求直线l 的 斜率k 的取值范围;
斜率k 的取值范围; 能否
能否 等于120°?若能,求出相应的直线l 的方程;若不能,请说明理由.
等于120°?若能,求出相应的直线l 的方程;若不能,请说明理由.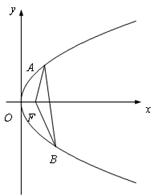
(本小题满分14分)
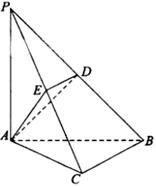
如图,四棱锥P-ABCD的底面为矩形,侧面PAD是正三角形,且侧面PAD⊥底面ABCD
(I) 求证:平面PAD⊥平面PCD
(II) 试在平面PCD上确定一点 E 的位置,使 |\S\UP6(→| 最小,并说明理由;
 (III) 当AD = AB时,求二面角A-PC-D的余弦值.
(III) 当AD = AB时,求二面角A-PC-D的余弦值.
一、选择题:本大题共12小题,每小题5分,共60分。
1―6AABCBD 7―12ACDCBD
二、填空题:本大题共4小题,每小题5分,共20分。
13.60° 14.-8 15. 16.6
16.6
三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分10分)
(I)解:因为
由正弦定理得
所以
又
故 5分
5分
(II)由
故
 10分
10分
18.(本小题满分12分)
(I)解:当
故 1分
1分
因为 当
当
故 上单调递减。
5分
上单调递减。
5分
(II)解:由题意知 上恒成立,
上恒成立,
即 上恒成立。
7分
上恒成立。
7分
令
因为 9分
9分
故 上恒成立等价于
上恒成立等价于
 11分
11分
解得 12分
12分
19.(本小题满分12分)
(I)证明:
 2分
2分
又
|