
题目列表(包括答案和解析)
| x |
A、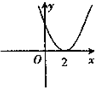 |
B、 |
C、 |
D、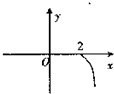 |
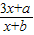 图象上有两个关于原点对称的不动点,求a,b应满足的条件;
图象上有两个关于原点对称的不动点,求a,b应满足的条件;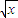 (x≥0),则其反函数f-1(x)的图象是( )
(x≥0),则其反函数f-1(x)的图象是( )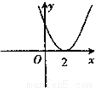
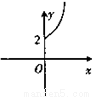
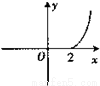
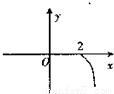
 (x≥0),则其反函数f-1(x)的图象是
(x≥0),则其反函数f-1(x)的图象是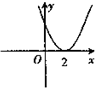
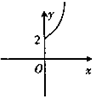
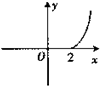
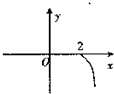
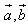 的夹角为锐角”的充要条件是“
的夹角为锐角”的充要条件是“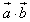 >0”;
>0”;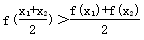 ;
;1.D 2.D 3.D 4.D 5.B 6.C 7.C 8.C 9.B 1 0.C 11.A 12.B
13. 14.
14. 15.
15. 16.
16.
提示:
1.D 由 ,得
,得 ,所以焦点
,所以焦点
2.D 解不等式 ,得
,得 ,∴
,∴ ,
,
∴ ,故
,故
3.D (法一)当 时,
时, 推导不出
推导不出 ,排除C;故选D。
,排除C;故选D。
(法二)∵ ,
, 为非零实数且满足
为非零实数且满足 ,∴
,∴ ,即
,即 ,故选D。
,故选D。
4.D  ,
, ,∴
,∴ ,∴
,∴ .
.
5.B 两式相减得 ,∴
,∴ ,∴
,∴ .
.
6.C 令 ,解得
,解得 ,∴
,∴ .
.
7.C 可知四面体 的外接球以
的外接球以 的中点
的中点 为球心,故
为球心,故
8.C 由已知有 或
或 解得
解得 或
或
9.B  ,∴
,∴ ,又
,又 ,
,
∴切线 的方程为
的方程为 ,即
,即 ,∴点
,∴点 到直线
到直线 的距离为期不远
的距离为期不远
10.C 对于A、D, 与
与 ,
, 不是对称轴;对于B,电
不是对称轴;对于B,电 不是偶函数;对于C,
不是偶函数;对于C, 符合要求.
符合要求.
11.A 由题意知直线 的方程为
的方程为 ,当
,当 时,
时, ,即点
,即点 是渐近线
是渐近线 上一点,∴
上一点,∴ ,即离心率
,即离心率 .
.
12. B 应先求出2人坐进20个座位的排法。排除2人相邻的情况即可。
共有11+12=23个座位,去掉前排中间3个不能入坐的座位,还有20个座位,则2人坐入20个座位的排法有 种,排除①两人坐前排相邻的12种情况;②两人坐后排相邻的22种情况,∴不同排法的种数有
种,排除①两人坐前排相邻的12种情况;②两人坐后排相邻的22种情况,∴不同排法的种数有 (种).
(种).
13. 展开式中的
展开式中的 的系数是
的系数是 ,
,
14.800 由图知成绩在 中的频率为
中的频率为 ,所以在10000人中成绩在
,所以在10000人中成绩在 中的人有
中的人有 人。
人。
15. 设棱长均为2,由图知
设棱长均为2,由图知 与
与 到
到 的距离相等,而
的距离相等,而 到平面
到平面 的距离为
的距离为 ,故所成角的正弦值为
,故所成角的正弦值为 。
。

16. 求圆面积的最大值,即求原点到三条直线
求圆面积的最大值,即求原点到三条直线 ,
, 和
和 距离的最小值,由于三个距离分别为
距离的最小值,由于三个距离分别为 、
、 、
、 ,最小值为
,最小值为 ,所以圆面积的最大值为
,所以圆面积的最大值为 。
。
17.解:(1)由 ,得
,得 ,…2分
,…2分
∴ ,∵
,∵ ,∴
,∴ ,∴
,∴
…………………………………………………………………………4分
∵ ,∴
,∴ ………………………………………5分
………………………………………5分
(2)∵ ,∴
,∴ ,
,
∴
 ……………8分
……………8分
∵ ,∴
,∴ ,∴
,∴ ……………10分
……………10分
18.解:(1)证明:延长 、
、 相交于点
相交于点 ,连结
,连结 。
。
∵ ,且
,且 ,∴
,∴ 为
为 的中点,
的中点, 为
为 的中点。
的中点。
∵ 为
为 的中点,由三角形中位线定理,有
的中点,由三角形中位线定理,有
∵ 平面
平面 ,
, 平面
平面 ,∴
,∴ 平面
平面 …………………6分
…………………6分
(2)(法一)由(1)知平面 平面
平面 。
。
∵ 为
为 的中点,∴取
的中点,∴取 的中点
的中点 ,则有
,则有 。
。
∵ ,∴
,∴
∵ 平面
平面 ,∴
,∴ 为
为 在平面
在平面 上的射影,∴
上的射影,∴
∴ 为平面
为平面 与平面
与平面 所成二面角的平面角。……………………10分
所成二面角的平面角。……………………10分
∵在 中,
中, ,
, ,
,
∴ ,即平面
,即平面 与平面
与平面 所成二面角的大小为
所成二面角的大小为 。…………12分
。…………12分
(法二)如图,∵ 平面
平面 ,
, ,
,
∴ 平面
平面 ,
,
取 的中点
的中点 为坐标原点,以过
为坐标原点,以过 且平行
且平行 的直线为
的直线为 轴,
轴, 所在的直线为
所在的直线为 轴,
轴, 所在的直线为
所在的直线为 轴,建立空间直角坐标系。
轴,建立空间直角坐标系。
设 ,则
,则 ,
, ,
, ,
, ,
,
∴ ,
,
 设
设 为平面
为平面 的法向量,
的法向量,
则

取 ,可得
,可得
又平面 的法向量为
的法向量为 ,设
,设 与
与 所成的角为
所成的角为 ,………………… 8分
,………………… 8分
则 ,
,
由图可知平面 与平面
与平面 所成二面角为锐角。
所成二面角为锐角。
∴平面 与平面
与平面 所成二面角的大小为
所成二面角的大小为 ………………………………12分
………………………………12分
19.解:(1)由已知得 ,∵
,∵ ,∴
,∴
∵ 、
、 是方程
是方程 的两个根,∴
的两个根,∴
∴ ,
, …………………………………………6分
…………………………………………6分
(2)设两台电器无故障使用时间分别为 、
、 ,则销售利润总和为200元有三种情况:
,则销售利润总和为200元有三种情况:
 ,
, ;
; ,
, ;
; ,
, ,
,
其概率分别为 ;
; ;
;
∴销售两台这种家用电器的销售利润总和为200元的概率为
………………………12分
20.解:(1)∵ ,且
,且 的图象经过点
的图象经过点 ,
, ,
,
∴ ∴
∴
∴
由图象可知函数 在
在 上单调递减,在
上单调递减,在 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,
∴ ,解得
,解得 ,
,
∴ ………………………6分
………………………6分
(2)要使对 都有
都有 恒成立,只需
恒成立,只需 即可。
即可。
由(1)可知函数 在
在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
在 上单调递减,且
上单调递减,且 ,
, ,、
,、
∴ ,
,
 ,
,
故所求的实数 的取值范围为
的取值范围为 ………………………12分
………………………12分
21.解:(1)∵ ,∴
,∴ ,∴
,∴
又∵ ,∴数列
,∴数列 是首项为1,公比为3的等比数列,
是首项为1,公比为3的等比数列,
 。
。
当 时,
时, (
( ),∴
),∴

(2) ,
,
当 时,
时, ;
;
当 时,
时, ,①
,①
 ②
②
①-②得:

∴
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com