
题目列表(包括答案和解析)
| x |
| 1+|x| |
| x |
| 1+n|x| |
| x |
| 1+|x| |
| x |
| 1+n|x| |
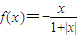 (x∈R)时,分别给出下面四个结论:
(x∈R)时,分别给出下面四个结论: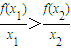 ;
;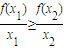 ;
;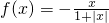 (x∈R)时,分别给出下面四个结论:
(x∈R)时,分别给出下面四个结论: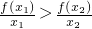 ;
;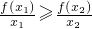 ;
;四位同学在研究函数f(x)=![]() (x∈R)时,分别给出下面四个结论:
(x∈R)时,分别给出下面四个结论:
①函数f(x)的图象关于y轴对称;
②函数f(x)的值域为(-1,1);
③若x1≠x2,则一定有f(x1)≠f(x2);
④若规定f1(x)=f(x),fn+1(x)=f[fn(x)],则fn(x)=![]() 对任意n∈N*恒成立.你认为上述四个结论中正确的有________
对任意n∈N*恒成立.你认为上述四个结论中正确的有________
一、选择题
|