练习册

  • 练习册
  • 试题
    已知圆的方程为．圆内一点P 【查看更多】

     

    题目列表(包括答案和解析)

    已知圆的方程为（x-1）2+（y-1）2=9，P（2，2）是该圆内一点，过点P的最长弦和最短弦分别为AC和BD，则四边形ABCD的面积是（　　）

    查看答案和解析>>

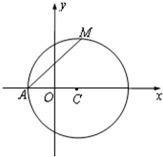    精英家教网已知圆C：（x-1）2+y2=r2（r＞1），设A为圆C与x轴负半轴的交点，过点A作圆C的弦AM，并使弦AM的中点恰好落在y轴上．
    （1）当r在（1，+∞）内变化时，求点M的轨迹E的方程；
    （2）设轨迹E的准线为l，N为l上的一个动点，过点N作轨迹E的两条切线，切点分别为P，Q．求证：直线PQ必经过x轴上的一个定点B，并写出点B的坐标．

    查看答案和解析>>

    已知圆O：x2+y2=4内一点P（0，1），过点P的直线l交圆O于A，B两点，且满足
    AP
    =λ
    PB
    （λ为参数）．
    （1）若|AB|=
    		14
    ，求直线l的方程；
    （2）若λ=2，求直线l的方程；
    （3）求实数λ的取值范围．

    查看答案和解析>>

    已知圆C：（x+l）2+y2=8及点F（l，0），P为圆C上一动点，在同一坐标平面内的动点M满足：
    CM
    ∥
    CP
    ，|
    MF
    |=|
    MP
    |    ．
    （I）求动点M的轨迹E的方程；
    （II）过点F作直线l与（I）中轨迹E交于不同两点R、S，设
    FR
    =λ
    FS
    ，λ∈[-2，-1)    ，求直线l 的纵截距的取值范围．

    查看答案和解析>>

    已知圆C：x2+y2+2x-4y+k=0（k＜5）；
    （I）若k=1，圆C内有一点P0（-2，3），经过P0的直线l与圆C交于A、B两点，当弦AB恰被P0平分时，求直线l的方程；
    （II）若圆C与直线x+y+1=0交于P、Q两点，是否存在实数k，使OP⊥OQ（O为原点）？如果存在，求出k的值；如果不存在，说明理由．

    查看答案和解析>>

    一.   选择题：

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    答案

    C

    D

    A

    B

    D

    D

    D

    C

    A

    D

    二、填空题（4分×5=20分）

    11、(x-2)2+(y+1)2=4  12、b>a>c   13、或

    14、2   15、(2)(3)

    三．解答题:

    16.解：(1).M={1，2}，N={0，1，2，3}……………………….2 分

    MN={1,2}………………………………………………….    4分

    (2). MQ

    当a2+1=2即a=1或-1时, a=1Q={1,2,2}(舍)a=1符合题意;……6分

    当a+1=2即a=1时, Q={1,1,1}(舍)……………………………..8分

     a=－1……………………………………………………………9分

    17. 解：（1）得      交点P( 0,2  )……….. 3 分

    （2）与直线L3:3x-4y+5=0平行的直线方程: ……………6分

    与直线L3:3x-4y+5=0垂直的直线的方程…………………9分

    18. 解：(1). f(2)=      f()=………………………………………….1分

    f(3)=       f()=…………………………………………2分

    (2) f(x) +f()=1…………………………………………………………3分

    f(x) +f()=+=1 ………………………………………6分

    (3). f(1)+f(2)+f(3)+=……10分

    19. EF是的中位线

    又

             ………………………………………………………5分

        ………………………………………………………10分

    20.（1）。直线EF的方程：x+y-8=0    ………………………………………………..2分

    EF=2=7  ………………………………………………………5分

    （2）。最长的弦长为10，最短的弦长为4  ………………………………………7分

    S=/AB//CD/=20………………………………………………………………..11分

    21、（1）。

    y=2x((0…………3分

    （2）

    ………………………………………..7分

    （3）每月0――15小时，选方案1；

    每月15――60小时，选方案2；

    每月60小时以上，选方案3。……………………………………………………..11分

     


    同步练习册答案