
题目列表(包括答案和解析)
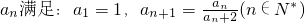 .
.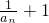 是等比数列;
是等比数列;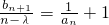 ,且数列{bn}是单调递增数列,求实数λ的取值范围.
,且数列{bn}是单调递增数列,求实数λ的取值范围.已知![]() 是等差数列,
是等差数列,![]() 是公比为q的等比数列,
是公比为q的等比数列,![]() ,记
,记![]() 为数列
为数列![]() 的前n项和。
的前n项和。
(1)若![]() (
(![]() 是大于2的正整数)。求证:
是大于2的正整数)。求证:![]() ;
;
(2)若![]() (i是某个正整数,求证:q是整数,且数列
(i是某个正整数,求证:q是整数,且数列![]() 中的每一项都是数列
中的每一项都是数列![]() 中的项。
中的项。
(3)是否存在这样的正数q,使等比数列![]() 中有三项成等差数列?若存在,写出一个q的值,并加以说明,若不存在,请说明理由。
中有三项成等差数列?若存在,写出一个q的值,并加以说明,若不存在,请说明理由。
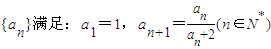 .
.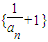 是等比数列;
是等比数列;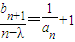 ,且数列{bn}是单调递增数列,求实数λ的取值范围.
,且数列{bn}是单调递增数列,求实数λ的取值范围.
一、选择题:本大题共12小题,每小题5分,共60分。
ABBD DABD BCCA
二、填空题:本大题共4小题,每小题4分,共16分。
13. 14.3 15.
14.3 15. 16.①③
16.①③
三、解答题:本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。
17.解:(I) ………2分
………2分
依题意函数
所以 …………4分
…………4分

(II)

18.解:(I)由题意得:上年度的利润的 万元;
万元;
本年度每辆车的投入成本为 万元;
万元;
本年度每辆车的出厂价为 万元;
万元;
本年度年销售量为 ………………2分
………………2分
因此本年度的利润为

(II)本年度的利润为

………………7分
则
由 (舍去)。 …………9分
(舍去)。 …………9分
|