
题目列表(包括答案和解析)
(07年山东卷理)(14分)设函数![]() ,其中
,其中![]() .
.
(I)当![]() 时,判断函数
时,判断函数![]() 在定义域上的单调性;
在定义域上的单调性;
(II)求函数![]() 的极值点;
的极值点;
(III)证明对任意的正整数![]() ,不等式
,不等式![]() 都成立.
都成立.
(04年天津卷理)(12分)
已知定义在R上的函数![]() 和数列
和数列![]() 满足下列条件:
满足下列条件:
![]() ,
,
![]()
其中![]() 为常数,
为常数,![]() 为非零常数。
为非零常数。
(I)令![]() ,证明数列
,证明数列![]() 是等比数列;
是等比数列;
(II)求数列![]() 的通项公式;
的通项公式;
(III)当![]() 时,求
时,求![]()
(本题满分14分)
已知![]() 为
为![]() 三点所在直线外一点,且
三点所在直线外一点,且![]() .数列
.数列![]() ,
,![]() 满足
满足![]() ,
,![]() ,且
,且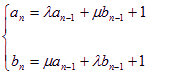 (
(![]() ).(Ⅰ) 求
).(Ⅰ) 求![]() ;(Ⅱ) 令
;(Ⅱ) 令![]() ,求数列
,求数列![]() 的通项公式;(III) 当
的通项公式;(III) 当![]() 时,求数列
时,求数列![]() 的通项公式.
的通项公式.
(本小题满分14分)
已知 函数
函数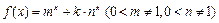 .
.
(I) 若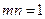 且函数
且函数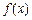 为奇函数,求实数
为奇函数,求实数 ;
;
(II) 若 试判断函数
试判断函数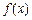 的单调性;
的单调性;
(III) 当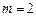 ,
, ,
,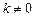 时,求函数
时,求函数 的对称轴或对称中心.
的对称轴或对称中心.
(本小题满分12分)
已知函数f(x)=x-ln(x+a).(a是常数)
(I)求函数f(x)的单调区间;
(II) 当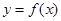 在x=1处取得极值时,若关于x的方程f(x)+2x=x2+b在[,2]上恰有两个不相等的实数根,求实数b的取值范围;
在x=1处取得极值时,若关于x的方程f(x)+2x=x2+b在[,2]上恰有两个不相等的实数根,求实数b的取值范围;
(III)求证:当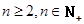 时
时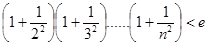 .
.
一、选择题:本大题共12小题,每小题5分,共60分。
ABBD DABD BCCA
二、填空题:本大题共4小题,每小题4分,共16分。
13. 14.3 15.
14.3 15. 16.①③
16.①③
三、解答题:本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。
17.解:(I) ………2分
………2分
依题意函数
所以 …………4分
…………4分

(II)

18.解:(I)由题意得:上年度的利润的 万元;
万元;
本年度每辆车的投入成本为 万元;
万元;
本年度每辆车的出厂价为 万元;
万元;
本年度年销售量为 ………………2分
………………2分
因此本年度的利润为

(II)本年度的利润为

………………7分
则
由 (舍去)。 …………9分
(舍去)。 …………9分
|