题目列表(包括答案和解析)
（）某工厂有工人1000名， 其中250名工人参加过短期培训（称为A类工人），另外750名工人参加过长期培训(称为B类工人），现用分层抽样方法（按A类、B类分二层）从该工厂的工人中共抽查100名工人，调查他们的生产能力（此处生产能力指一天加工的零件数）。
（I）求甲、乙两工人都被抽到的概率，其中甲为A类工人，乙为B类工人；
（II）从A类工人中的抽查结果和从B类工人中的抽插结果分别如下表1和表2.
表1：
| 生产能力分组 |
|
|
|
|
|
| 人数 | 4 | 8 |
| 5 | 3 |
表2：
| 生产能力分组 |
|
|
|
|
| 人数 | 6 | y | 36 | 18 |
（i）先确定x，y，再在答题纸上完成下列频率分布直方图。就生产能力而言，A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小？（不用计算，可通过观察直方图直接回答结论）
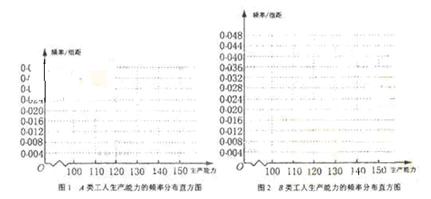
（ii）分别估计A类工人和B类工人生产能力的平均数，并估计该工厂工人的生产能力的平均数，同一组中的数据用该组区间的中点值作代表）
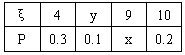
（本小题满分12分）
公安部发布酒后驾驶处罚的新规定（一次性扣罚12分）已于2011年4月1日起正式施行．酒后违法驾驶机动车的行为分成两个档次：“酒后驾车”和“醉酒驾车”，其检测标准是驾驶人员血液中的酒精含量
（简称血酒含量，单位是毫克/100毫升），当
时，为酒后驾车；当
时，为醉酒驾车．某市公安局交通管理部门在某路段的一次拦查行动中，依法检查了200辆机动车驾驶员的血酒含量（如下表）．
|
血酒含量 |
（0，20） |
[20,40） |
[40，60） |
[60，80） |
[80，100） |
[100，120] |
|
人数 |
194 |
1 |
2 |
1 |
1 |
1 |
依据上述材料回答下列问题：
（1）分别写出酒后违法驾车发生的频率和酒后违法驾车中醉酒驾车的频率；
（2）从酒后违法驾车的司机中，抽取2人，请一一列举出所有的抽取结果，并求取到的2人中含有醉酒驾车的概率． （酒后驾车的人用大写字母如
表示，醉酒驾车的人用小写字母如
表示）
（本小题满分12分）
公安部发布酒后驾驶处罚的新规定（一次性扣罚12分）已于2011年4月1日起正式施行．酒后违法驾驶机动车的行为分成两个档次：“酒后驾车”和“醉酒驾车”，其检测标准是驾驶人员血液中的酒精含量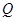
（简称血酒含量，单位是毫克/100毫升），当
时，为酒后驾车；当
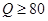时，为醉酒驾车．某市公安局交通管理部门在某路段的一次拦查行动中，依法检查了200辆机动车驾驶员的血酒含量（如下表）．
| 血酒含量 | （0，20） | [20,40） | [40，60） | [60，80） | [80，100） | [100，120] |
| 人数 | 194 | 1 | 2 | 1 | 1 | 1 |
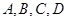表示，醉酒驾车的人用小写字母如
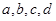表示）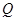 
（简称血酒含量，单位是毫克/100毫升），当
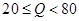时，为酒后驾车；当
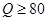时，为醉酒驾车．某市公安局交通管理部门在某路段的一次拦查行动中，依法检查了200辆机动车驾驶员的血酒含量（如下表）．| 血酒含量 | （0，20） | [20,40） | [40，60） | [60，80） | [80，100） | [100，120] |
| 人数 | 194 | 1 | 2 | 1 | 1 | 1 |
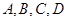表示，醉酒驾车的人用小写字母如
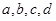表示） 一、选择题
题号
1
2
3
4
5
6
7
8
答案
D
A
C
B
D
C
C
A
4．【解析】{an}为等差数列，则{
}也为等差数列且其公差d
= 1,
∴
，∴
=
．
5．【解析】圆方程可化为
，则圆心到直线的距离
，当1＜d＜3时，则圆上恰有两个点到直线的距离等于1，
＜|c|＜
，故选D.
6．【解析】y
= f(x)是奇函数，由f(x)＞f (?x) + x得f(x)＞
，数形结合．
7．【解析】设l过原点，取线段AB的中点M(?1，
)，则OM⊥l，∴kl =
．
8．【解析】∵f(x)是偶函数且f(x)在[0，+∞)是增函数
∴|ax + 1|≤|x ?2|恒成立，x∈[
，1]．
∴x ? 2≤ax + 1≤2 ? x
即
．
二、填空题
9．【解析】
，令
有r = 2，∴
．
10．【解析】
= 1440．
11． 【解析】求出交点
代入求出k并验证得k = ?9．
12．
【解析】易求：抛物线焦点F(4，0)，准线L：x = ? 4．椭圆焦点F(4，0)、 F′(4，4)，如图所示．
所以F为两曲线之公共焦点．
设两曲线交于点A，则
所以当H、A、F′共线时，2a有最小值，从而a也达到最小，此时，yA = yF = 4，代入y2 = 16x 得xA = 1，再以A(1，4)代入椭圆得：a2 = 16，从而a = 4．
13．【解析】①在平面A′FA内过点A′作A′H⊥AF，垂足为H，由DE⊥AF，DE⊥A′G知DE⊥平面A′GA．故DE⊥A′H，∴A′H⊥平面ABC，即A′在平面ABC上的射影在线段AF上．
②由①得；
③由①知：当A′H与A′G重合时，三棱锥A′―FED的体积有最大值；
④用反证法：假设A′E与BD垂直，由①知A′H⊥BD，∴BD⊥面A′HE，EH⊥BD．
∴当EH⊥BD时，可证A′E⊥BD．
故①②③正确．
14．【解析】当n≤x＜n + 1(n∈Z)时，y = f(x) = x ? n，
显然有0≤x ? n＜1，即0≤y＜1，
也有f(x+ 1) }= x + 1 ? [x + 1] = x + 1? ([x] + 1) = x ? [x] = f(x)．如图．
答案为：［0，1）；1
15．【解析】（i）20；
（ii）将粒子的运动轨迹定义为数对（i，j）
则它的运动整点可排成数表
（0，0）
（0，1） （1，1） （1，0）
（0，0） （2，1） （2，2） （1，2） （0，2）
（0，3） （1，3） （2，3） （3，3） （3，2） （3，1） （3，0）
（4，0） （4，1） （4，2） （4，3） （4，4） （3，4） （2，4） （1，4）（0，4）
通过推并可知：经过2 = 1×2s，运动到（1，1）
经过6 =2×3s，运动到（2，2）
经过12 =3×4s，运动到（3，3）
∴经过44×45 = 1980s，运动到（44，44）
再继续运动29s，到达点（15，44）．
三、解答题
16．【解析】（1）
= 0，1，2，4．
（1分）
P(=
4) =
P(=
2) =
P(=
1) =
P(=
0) = 1?P(=
1) ?P(=
2) ?P(=
4) =
（7分）
∴的分布列为
0
1
2
4
P
（9分）
∴E=
，
D=
(0 ? 1)2×+ (1 ? 1)2×+(2 ? 1)2×+(4 ? 1)2×= 1
（12分）
17．【解析】（Ⅰ）∵
，∴
= 0，
（2分）
∴
，
（4分）
又∵
∈R，∴
时，mmin = ?2.
又
，所以
（6分）
（Ⅱ）∵
，且
,∴
（8分）
∴
∴
（10分）
（12分）
18．【解析】（Ⅰ）∵AB = 3，BC = 4，∴AC = 5
∵AC2 = AB2 + BC2
∴AB⊥BC
又AB⊥BB1
且BC∩BB1 = B
∴AB⊥面BCC1B1 （4分）
（Ⅱ）如图，建立空间直角坐标系
则A(3，0，0)，P(0，0，3)，Q(0，4，4)
设面APQ的法向量为
= (x，y，z)
= (1，?1，1)
而面ABC的法向量可以取
= (0，0，1)
∴
∴面PQA与面ABC所成的锐二面角为arccos
．
（8分）
（Ⅲ）∵BP = AB = 3，CQ = AC = 7．
∴S四边形BCQP
=
∴VA―BCQP
=×20×3 = 20
又∵V
=
．
∴
．
（12分）
19．【解析】（Ⅰ）
（
）． （2分）
（Ⅱ）设第n区内的面积为bn平方米，
则 
． （4分）
则第n区内火山灰的总重量为
（吨）
（万吨） （6分）
设第n区火山灰总重量最大，则
解得
∴n =50.
即得第50区火山灰的总重量最大. （9分）
（Ⅲ）设火山喷发的火山区灰总重量为S万吨，
则
设
则
①
∴
②
①－②得
∴
（12分）
∵0＜q＜1，∴
（万吨）
因此该火山这次喷发出的火山灰的总重量约为3712万吨． （13分）
20．【解析】（Ⅰ）因为圆O的方程为x2 + y2
= 2，所以d
=
，
可得b2 = 2(k2 + 1)(k≠±1)． （4分）
（Ⅱ）设A(x1，y1)，B(x2，y2)，
由
，
所以
，
（7分）
所以
=
=
，
因为|AB| =
×
=
，
O到AB的距离
，
（11分）
所以
=
∈
．
（13分）
21．（Ⅰ）【解析】
．
（2分）
由f (?2) =
又∵b，c∈N* ∴c = 2，b = 2
∴f (x) =
．
（4分）
令f′(x)＞0得：x＜0或x＞2
令f′(x)＜0得：0＜x＜2
∴f(x)的单调递增区间为（?∞，0），（2，+∞）
f(x)的单调递减区间为（0，1），（1，2）． （6分）
（Ⅱ）证明：由已知可得：2Sn = an ? 
，
两式相减得：(an + an ? 1) (an ? an ? 1+1) = 0 （n≥2）
∴an = ?an ?1或an ?an?1 = ?1 （7分）
当n =1 时，2a1 = a1 ?
若an = ?an?1，则a2 = ?a1 = 1与an≠1矛盾．
（定义域要求an≠1）
∴an ? an?1 = 1，∴an = ?n． （8分）
要证的不等式转化为
先证不等式
令g (x) = x ?ln(1 + x)，h(x) = ln(x +1) ?
（10分）
则g′(x) =
，h′(x) =
∵x＞0 ∴g′(x)＞0，h′(x)＞0
∴g (x)， h(x)在（0，+∞）上
∴g (x)＞g (0) = 0，h(x)＞h(0) = 0 （12分）
∴
故
，即
．
（13分）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
