17．如图所示.处于匀强磁场中的两根足够长.电阻不计的平行金属导轨相距=1m.导轨平面与水平面成角.下端连接阻值为的电阻.匀强磁场方向与导轨平面垂直.质量为=0.2kg.电阻不计的金属棒放在两导轨上.——青夏教育精英家教网—

17．如图所示.处于匀强磁场中的两根足够长.电阻不计的平行金属导轨相距=1m.导轨平面与水平面成角.下端连接阻值为的电阻.匀强磁场方向与导轨平面垂直.质量为=0.2kg.电阻不计的金属棒放在两导轨上.棒与导轨垂直并保持良好接触.它们之间的动摩擦因数为.(设最大静摩擦力大小等于滑动摩擦力大小.且g取10m/s2.sin37°=0.6,cos37°=0.8).求: (1)金属棒沿导轨由静止开始下滑时加速度a的大小【查看更多】

题目列表(包括答案和解析)

如图所示，处于匀强磁场中的两根足够长、电阻不计的光滑平行金属导轨相距L=1m，导轨平面与水平面成θ=30°角，下端连接阻值为R=0.8Ω的电阻，匀强磁场方向与导轨平面垂直，磁感强度大小B=1T；质量为m=0.1kg、电阻r=0.2Ω金属棒放在两导轨上，棒与导轨垂直并保持良好接触．g取10m/s²．求：
（1）金属棒沿导轨由静止开始下滑时的加速度大小；
（2）金属棒ab所能获得的最大速度；
（3）若属棒ab沿斜面下滑0.2m时恰好获得最大速度，求在此过程中回路一共生热多少焦？

查看答案和解析>>

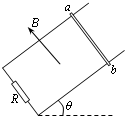如图所示，处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距l=1.0m，导轨平面与水平面成θ=37°角，下端连接阻值为R=2.0Ω的电阻，匀强磁场方向与导轨平面垂直，磁感应强度的大小B=0.40T．质量为m=0.20kg、电阻不计的金属棒放在两导轨上，棒与导轨垂直并保持良好接触，它们之间的动摩擦因数为μ=0.25．
（1）求金属棒沿导轨由静止开始下滑时的加速度大小；
（2）求金属棒下滑速度达到稳定时的速度大小．（g=10m/s²，sin37°=0.6，cos37°=0.8）

查看答案和解析>>

如图所示，处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距l=1m，导轨平面与水平面成θ=37°角，下端连接阻值R=2Ω的电阻．匀强磁场的磁感应强度B=0.4T，方向垂直导轨平面向上．质量为m=0.2kg、电阻不计的金属棒ab放在两导轨上，棒与导轨垂直并保持良好接触，它们之间的动摩擦因数为μ=0.25．求：
（1）金属棒沿导轨由静止开始下滑时的加速度大小；
（2）当金属棒下滑速度达到稳定时，金属棒速度的大小；
（3）已知金属棒下滑时间为t=4s时，运动路程为s=20m，其速度为v=8m/s．若在这4s内，R产生的热与一恒定电流I₀在R内产生的热量相同，求恒定电流I₀的值．

查看答案和解析>>

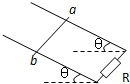如图所示，处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距L=1m，导轨平面与水平面成θ=37°角，下端连接阻值为R的电阻．匀强磁场方向与导轨平面垂直．质量为m=0.2kg，电阻不计的金属棒放在两导轨上，棒与导轨垂直并保持良好接触，它们之间的动摩擦因数为μ=0.25．（设最大静摩擦力大小等于滑动摩擦力大小）求：
（1）金属棒沿导轨由静止开始下滑时加速度a的大小；
（2）当金属棒下滑速度达到稳定时，电阻R消耗的功率为8W，求此时金属棒速度v的大小；
（3）在上问中，若R=2Ω，金属棒中的电流方向由a到b，求磁感应强度B的大小和方向．（g=10m/s²，sin37°=0.6，cos37°=0.8）

查看答案和解析>>

如图所示，处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距L，导轨平面与水平面成θ角，下端连接阻值为R的电阻．匀强磁场方向与导轨平面垂直．质量为m，电阻不计的金属棒放在两导轨上，棒与导轨垂直并保持良好接触，它们之间的动摩擦因数为μ，求：
（1）金属棒沿导轨由静止开始下滑过程中，加速度的最大值．
（2）当金属棒下滑速度达到稳定时，电阻R消耗的功率为P，求磁感应强度的大小．

查看答案和解析>>

一、选择题：本题共10小题，每小题4分，共40分。在每个小题给出的四个选项中至少有一个选项符合题目要求，选全的得4分，选对但不全的得２分，选错和不选的得０分。

1.D 2.C 3.BD 4.A 5.D 6.BD 7.D 8.D 9.A 10.C

二、实验题：本题共4个小题,满分23分,把答案直接填在题中的相应位置。

11. A C （3分）

12. A B D （3分）