
题目列表(包括答案和解析)
(本小题满分14分)
如图,过抛物线 上一点P(
上一点P( ),作两条直线分别交抛物线于A(
),作两条直线分别交抛物线于A( ),B(
),B( ).直线PA与PB的斜率存在且互为相反数,(1)求
).直线PA与PB的斜率存在且互为相反数,(1)求 的值,(2)证明直线AB的斜率是非零常数.
的值,(2)证明直线AB的斜率是非零常数.
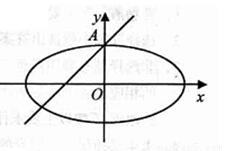
(本小题满分14分)如图所示,椭圆 的离心率为
的离心率为 ,且A(0,1)是椭圆C的顶点。
,且A(0,1)是椭圆C的顶点。
(1)求椭圆C的方程;
(2)过点A作斜率为1的直线 ,设以椭圆C的右焦点F为抛物线
,设以椭圆C的右焦点F为抛物线 的焦点,若点M为抛物线E上任意一点,求点M到直线
的焦点,若点M为抛物线E上任意一点,求点M到直线 距离的最小值。
距离的最小值。
(本小题满分14分)
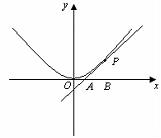
如图,已知直线![]() 与抛物线
与抛物线![]() 相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0)。
相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0)。
 (1)若动点M满足
(1)若动点M满足![]() ,求动点M的轨迹C的方程;
,求动点M的轨迹C的方程;
(2)若过点B的直线![]() (斜率不等于零)与(1)中的轨迹C交于不同
(斜率不等于零)与(1)中的轨迹C交于不同
的两点E、F(E在B、F之间),且![]() ,试求
,试求![]() 的取值范围。
的取值范围。
(本小题满分14分)
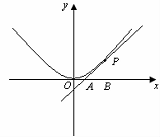
如图,已知直线![]() 与抛物线
与抛物线![]() 相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0)。
相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0)。
 (1)若动点M满足
(1)若动点M满足![]() ,求动点M的轨迹C的方程;
,求动点M的轨迹C的方程;
(2)若过点B的直线![]() (斜率不等于零)与(1)中的轨迹C交于不同
(斜率不等于零)与(1)中的轨迹C交于不同
的两点E、F(E在B、F之间),且![]() ,试求
,试求![]() 的取值范围。
的取值范围。
(本小题满分14分)
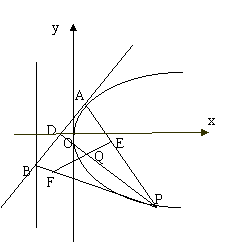 如图:过抛物线
如图:过抛物线![]() 上的点A(1,2)作切线
上的点A(1,2)作切线![]() 交
交![]() 轴与直线
轴与直线![]() 分别于D,B. 动点P是抛物线
分别于D,B. 动点P是抛物线![]() 上的一点,点E在线段AP上,满足
上的一点,点E在线段AP上,满足![]() ;点F在线段BP上,满足
;点F在线段BP上,满足![]() ,
,![]() 且在
且在![]() 中,线段PD与EF交于点Q.
中,线段PD与EF交于点Q.
(1)求点Q的轨迹方程;
(2)若M,N是直线![]() 上的两点,且
上的两点,且
⊙![]() :
:![]() 是
是![]() 的内切圆,
的内切圆,
试求![]() 面积的取值范围。
面积的取值范围。
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
答案
C
A
B
B
C
D
C
D
B
A
二、填空题:
11. (-∞,0)∪(2,+∞), (2,+∞) (第一空3分,第二空2分)
12.
 13. π 14. (1,e), e (第一空3分,第二空2分)
13. π 14. (1,e), e (第一空3分,第二空2分)
三、解答题(共80分)解答应写出文字说明,证明过程或演算步骤.
15、解:(1) 等差数列
等差数列 中
中 ,公差
,公差

 ………………………………………………………4分
………………………………………………………4分
(2)  ………………………………………………………6分
………………………………………………………6分

 …………………8分
…………………8分
 ……………………………10分
……………………………10分



 .
………………………………………………………12分
.
………………………………………………………12分
16、解:(1)共有 种结果; ………………………………………………………4分
种结果; ………………………………………………………4分
(2)共有12种结果; ………………………………………………………8分
(3) .
………………………………………………………12分
.
………………………………………………………12分
17、解:(1) ,
,  .
.

 ………………………………………………………2分
………………………………………………………2分
 ………………………………………………………4分
………………………………………………………4分
 ………………………………………………………6分
………………………………………………………6分
 或
或

 或
或 
 所求解集为
所求解集为 ………………………………………8分
………………………………………8分
(2)

 …………………………………………………………………10分
…………………………………………………………………10分
 的增区间为
的增区间为
 ………………………………………………………12分
………………………………………………………12分

 原函数增区间为
原函数增区间为
 ………………………………………14分
………………………………………14分
18、(1)证明:连结 、
、 交于点
交于点 ,再连结
,再连结 ………………………………………………1分
………………………………………………1分

 且
且 , 又
, 又 ,
,
 且
且
 四边形
四边形 是平行四边形,
是平行四边形, …………… 3分
…………… 3分
又 面
面
 面
面 ……………………………… 4分
……………………………… 4分
(2)证明: 底面是菱形,
底面是菱形,  ………… 5分
………… 5分
又 面
面 ,
, 面
面
 ,
, 面
面 ………………………………………………6分
………………………………………………6分
又
 面
面 ………………………………………………8分
………………………………………………8分
(3)延长 、
、 交于点
交于点 ………………………………………………9分
………………………………………………9分
 是
是 的中点且
的中点且 是菱形
是菱形

又
 ……………………………………………………10分
……………………………………………………10分
由三垂线定理可知 
 为所求角 …………………………………………………………12分
为所求角 …………………………………………………………12分
在菱形 中,
中,


 …………………………………………………………14分
…………………………………………………………14分
19、解: …………………………………………………………2分
…………………………………………………………2分
(1)由题意: ……………………………………………………4分
……………………………………………………4分
解得 …………………………………………………………6分
…………………………………………………………6分
 所求解析式为
所求解析式为
(2)由(1)可得:
令 ,得
,得 或
或 ……………………………………………8分
……………………………………………8分
当 变化时,
变化时, 、
、 的变化情况如下表:
的变化情况如下表:









―



单调递增ㄊ

单调递减ㄋ

单调递增ㄊ
因此,当 时,
时, 有极大值
有极大值 …………………9分
…………………9分
 当
当 时,
时, 有极小值
有极小值 …………………10分
…………………10分
 函数
函数 的图象大致如图:……13分
y=k
的图象大致如图:……13分
y=k
由图可知: ………………………14分
………………………14分
20、解(Ⅰ)依题意,可设直线AB的方程为 ,
,
代入抛物线方程 得:
得: …………… ① …………………2分
…………… ① …………………2分
设A、B两点的坐标分别是(x1,y1)、(x2,y2),则x1、x2是方程①的两根.
 所以
所以
由点P(0,m)分有向线段 所成的比为
所成的比为 ,
,
得 ,
即
,
即 …………………4分
…………………4分
又点Q是点P关于原点的以称点,
故点Q的坐标是(0,--m),从而

=

=
=
=
=0,
所以 …………………………………………………………………………7分
…………………………………………………………………………7分
(Ⅱ)
由 得点A、B的坐标分别是(6,9)、(--4,4).
得点A、B的坐标分别是(6,9)、(--4,4).
由 得
得 ,
,

所以抛物线 在点A处切线的斜率为
在点A处切线的斜率为 .……………………………………………9分
.……………………………………………9分
设圆C的方程是 ,
,
则 ……………………………………………………11分
……………………………………………………11分
解之得  ………………………………………13分
………………………………………13分
所以圆C的方程是 .………………………………………………14分
.………………………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com