
题目列表(包括答案和解析)
数列![]() 的前n项和Sn,当
的前n项和Sn,当![]() 的等比中项
的等比中项![]()
(1)求证:对于![]() ;
;
(2)设![]() ,求Sn;
,求Sn;
(3)对![]() ,试证明:S1S2+S2S3+……+SnS
,试证明:S1S2+S2S3+……+SnS![]()
![]()
数列 的前n项和记为
的前n项和记为 ,前
,前 项和记为
项和记为
 ,对给定的常数
,对给定的常数 ,若
,若 是与
是与 无关的非零常数
无关的非零常数 ,则称该数列
,则称该数列 是“
是“ 类和科比数列”,
类和科比数列”,
(理科做以下(1)(2)(3))
(1)、已知 ,求数列
,求数列 的通项公式(5分);
的通项公式(5分);
(2)、证明(1)的数列 是一个 “
是一个 “ 类和科比数列”(4分);
类和科比数列”(4分);
(3)、设正数列 是一个等比数列,首项
是一个等比数列,首项 ,公比
,公比
 ,若数列
,若数列 是一个 “
是一个 “ 类和科比数列”,探究
类和科比数列”,探究 与
与 的关系(7分)
的关系(7分)
数列 的前n项和记为
的前n项和记为 ,
, ,点
,点 在直线
在直线 上,n∈N*.
上,n∈N*.
(1)求证:数列 是等比数列,并求数列
是等比数列,并求数列 的通项公式
的通项公式 ;
;
(2)设 ,
, 是数列
是数列 的前n项和,求
的前n项和,求 的值.
的值.
数列{ }的前n项和为
}的前n项和为 ,
, .
.
(Ⅰ)设 ,证明:数列
,证明:数列 是等比数列;
是等比数列;
(Ⅱ)求数列 的前
的前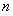 项和
项和 ;
;
(Ⅲ)若 ,数列
,数列 的前
的前 项和
项和 ,证明:
,证明:
 .
.
数列{ }的前n项和为
}的前n项和为 ,
, .
.
(Ⅰ)设 ,证明:数列
,证明:数列 是等比数列;
是等比数列;
(Ⅱ)求数列 的前
的前 项和
项和 ;
;
(Ⅲ)若 ,
, .求不超过
.求不超过 的最大整数的值.
的最大整数的值.

 又EG∩FG=G,∴面EFG//面BCO,∵EF
又EG∩FG=G,∴面EFG//面BCO,∵EF 面EFG,∴EF//面OBC。………6分
面EFG,∴EF//面OBC。………6分
(2)易求得 ….8分
….8分
设CF的延长线交OA的延长线于P,BE的延长线交OA的延长线于Q
 得
得
同理,直线OB的方程为 ,
,

 +
+
②当直线OA.OB的斜率有一条存在另一条不存在时,
或 ,
,
 也成立。
…………6分
也成立。
…………6分
(2)(1)的逆命题是:若 为定值,则
为定值,则 …7分
…7分
它是假命题 ….8分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com