
题目列表(包括答案和解析)
| p |
| q |
| 1 |
| 2 |
 )+
)+ =0,p,q∈R+},问是否存在p,q,使A∩B≠∅,若存在,求出p,q的值,不存在则说明理由.
=0,p,q∈R+},问是否存在p,q,使A∩B≠∅,若存在,求出p,q的值,不存在则说明理由.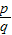 )+
)+ =0,p,q∈R+},问是否存在p,q,使A∩B≠∅,若存在,求出p,q的值,不存在则说明理由.
=0,p,q∈R+},问是否存在p,q,使A∩B≠∅,若存在,求出p,q的值,不存在则说明理由.设A,B为椭圆![]() 的两个动点,O为坐标原点.
的两个动点,O为坐标原点.
(1)证明:“若A,B满足![]() ,则
,则![]() 为定值”是真命题;
为定值”是真命题;
(2)(1)中的逆命题是否成立?证明你的结论.
| 1 |
| 2 |
| a+b |
| 2 |
| ab |

 又EG∩FG=G,∴面EFG//面BCO,∵EF
又EG∩FG=G,∴面EFG//面BCO,∵EF 面EFG,∴EF//面OBC。………6分
面EFG,∴EF//面OBC。………6分
(2)易求得 ….8分
….8分
设CF的延长线交OA的延长线于P,BE的延长线交OA的延长线于Q
 得
得
同理,直线OB的方程为 ,
,

 +
+
②当直线OA.OB的斜率有一条存在另一条不存在时,
或 ,
,
 也成立。
…………6分
也成立。
…………6分
(2)(1)的逆命题是:若 为定值,则
为定值,则 …7分
…7分
它是假命题 ….8分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com