
题目列表(包括答案和解析)
在“探究弹性势能的表达式”的活动中,为计算弹簧弹力所做功,把拉伸弹簧的过程分为很多小段,拉力在每小段可以认为是恒力,用各小段做功的代数和代表弹力在整个过程所做的功,物理学中把这种研究方法叫做“微元法”。下面几个实例中应用到这一思想方法的是( )
A.由加速度的定义 ,当
,当 非常小,
非常小, 就可以表示物体在t时刻的瞬时加速度
就可以表示物体在t时刻的瞬时加速度
B.在探究加速度、力和质量三者之间关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系
C.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加
D.在不需要考虑物体本身的大小和形状时,用有质量的点来代替物体,即质点
在“探究弹性势能的表达式”的活动中,为计算弹簧弹力所做功,把拉伸弹簧的过程分为很多小段,拉力在每小段可以认为是恒力,用各小段做功的代数和代表弹力在整个过程所做的功,物理学中把这种研究方法叫做“微元法”。下面几个实例中应用到这一思想方法的是( )
A.由加速度的定义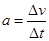 ,当 ,当 非常小, 非常小, 就可以表示物体在t时刻的瞬时加速度 就可以表示物体在t时刻的瞬时加速度 |
| B.在探究加速度、力和质量三者之间关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系 |
| C.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加 |
| D.在不需要考虑物体本身的大小和形状时,用有质量的点来代替物体,即质点 |
在“探究弹性势能的表达式”的活动中,为计算弹簧弹力所做功,把拉伸弹簧的过程分为很多小段,拉力在每小段可以认为是恒力,用各小段做功的代数和代表弹力在整个过程所做的功,物理学中把这种研究方法叫做“微元法”。下面几个实例中应用到这一思想方法的是
A.由加速度的定义![]() ,当
,当![]() 非常小,
非常小,![]() 就可以表示物体在t时刻的瞬时加速度
就可以表示物体在t时刻的瞬时加速度
B.在探究加速度、力和质量三者之间关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系
C.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加
D.在不需要考虑物体本身的大小和形状时,用有质量的点来代替物体,即质点
在“探究弹性势能的表达式”的活动中,为计算弹簧弹力所做功,把拉伸弹簧的过程分为很多小段,拉力在每小段可以认为是恒力,用各小段做功的代数和代表弹力在整个过程所做的功,物理学中把这种研究方法叫做“微元法”.下面几个实例中应用到这一思想方法的是
A.由加速度的定义a=![]() ,当Δt非常小,
,当Δt非常小,![]() 就可以表示物体在t时刻的瞬时加速度
就可以表示物体在t时刻的瞬时加速度
B.在探究加速度、力和质量三者之间关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系
C.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加
D.在不需要考虑物体本身的大小和形状时,用有质量的点来代替物体,即质点
一、不定项选择题:(本大题共10小题,每小题3分,共30分.全部选对得3分,部分选对得1分,选错或不答得0分)
1
2
3
4
5
6
7
8
9
10
C
AC
C
D
ABC
ACD
CD
ACD
BC
BD
二、填空、实验题:(本大题共4小题,共36分)
11.(6分) .files/image048.gif) 1.0
1.0
12.(12分)(1)甲 (2)BC (3)2.0 1.50 1.0 (6分)
|