(本小题满分16分)

设两个不共线的向量的夹角为，且，.

（1）若，求的值；

（2）若为定值，点在直线上移动，的最小值为，求的值.

（本小题满分16分）   已知二次函数。 （1）若是否存在为正数 ，若存在，证明你的结论，若不存在，说明理由；（2）若对有2个不等实根，证明必有一个根属于（3）若，是否存在的值使=成立，若存在，求出的取值范围，若不存在，说明理由。

（本小题满分16分）某连锁分店销售某种商品，每件商品的成本为4元，并且每件商品需向总店交a元（1≤a≤3）的管理费，预计当每件商品的售价为元（8≤x≤9）时，一年的销售量为(10－x)²万件．（1）求该连锁分店一年的利润L（万元）与每件商品的售价x的函数关系式L(x)；（2）当每件商品的售价为多少元时，该连锁分店一年的利润L最大，并求出L的最大值M(a)．

（本小题满分16分）

随机抽取某厂的某种产品400件，经质检，其中有一等品252件、二等品100件、三等品40件、次品8件．已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元，而1件次品亏损2万元．设1件产品的利润（单位：万元）为

（1）求的分布列和数学期望

（2）经技术革新后，仍有四个等级的产品，但次品率降为，一等品率提高为．如果此时要求1件产品的平均利润不小于4.73万元，则三等品率最多是多少？

（本小题满分16分）

已知f (x)、g(x)都是定义在R上的函数，如果存在实数m、n使得h (x) = m f(x)+ng(x)，那么称h (x)为f (x)、g(x)在R上生成的一个函数.

设f (x)=x²+ax，g(x)=x+b(R)，= 2x²+3x-1，h (x)为f (x)、g(x)在R上生成的一个二次函数.

（1）设，若h (x)为偶函数，求；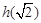

（2）设，若h (x)同时也是g(x)、l(x) 在R上生成的一个函数，求a+b的最小值；