
题目列表(包括答案和解析)
(本题满分18分,第1小题4分,第2小题6分,第3小题8分)
已知数列{an}满足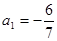 ,
,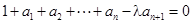 (其中λ≠0且λ≠–1,n∈N*),
(其中λ≠0且λ≠–1,n∈N*),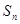 为数列{an}的前
为数列{an}的前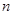 项和.
项和.
(1) 若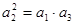 ,求
,求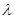 的值;
的值;
(2) 求数列{an}的通项公式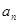 ;
;
(3) 当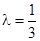 时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
(本题满分18分,第1小题4分,第2小题6分,第3小题8分)
已知数列{an}满足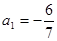 ,
, (其中λ≠0且λ≠–1,n∈N*),
(其中λ≠0且λ≠–1,n∈N*),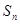 为数列{an}的前
为数列{an}的前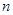 项和.
项和.
(1) 若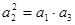 ,求
,求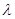 的值;
的值;
(2) 求数列{an}的通项公式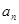 ;
;
(3) 当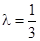 时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
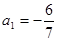 ,
,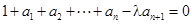 (其中λ≠0且λ≠–1,n∈N*),
(其中λ≠0且λ≠–1,n∈N*),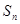 为数列{an}的前
为数列{an}的前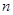 项和.
项和.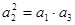 ,求
,求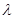 的值;
的值; ;
;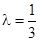 时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.(本题满分18分)第(1)小题满分4分,第(2)小题满分8分,第(3)小题满分6分。
定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”。如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比。已知椭圆![]() 。
。
若椭圆![]() ,判断
,判断![]() 与
与![]() 是否相似?如果相似,求出
是否相似?如果相似,求出![]() 与
与![]() 的相似比;如果不相似,请说明理由;
的相似比;如果不相似,请说明理由;
 写出与椭圆
写出与椭圆![]() 相似且短半轴长为
相似且短半轴长为![]() 的椭圆
的椭圆![]() 的方程;若在椭圆
的方程;若在椭圆![]() 上存在两点
上存在两点![]() 、
、![]() 关于直线
关于直线![]() 对称,求实数
对称,求实数![]() 的取值范围?
的取值范围?
如图:直线![]() 与两个“相似椭圆”
与两个“相似椭圆”![]() 和
和![]() 分别交于点
分别交于点![]() 和点
和点![]() ,证明:
,证明:![]()
(本题满分18分)第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分8分。
圆锥曲线上任意两点连成的线段称为弦。若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦。已知椭圆C:![]() 。
。
 (1)过椭圆C的右焦点作一条垂直于
(1)过椭圆C的右焦点作一条垂直于![]() 轴的垂轴弦
轴的垂轴弦![]() ,求
,求![]() 的长度;
的长度;
(2)若点![]() 是椭圆C上不与顶点重合的任意一点,
是椭圆C上不与顶点重合的任意一点,![]() 是椭圆C的短轴,直线
是椭圆C的短轴,直线![]() 分别交
分别交![]() 轴于点
轴于点![]() 和点
和点![]() (如右图),求
(如右图),求![]() 的值;
的值;
(3)在(2)的基础上,把上述椭圆C一般化为![]() ,
,![]() 是任意一条垂直于
是任意一条垂直于![]() 轴的垂轴弦,其它条件不变,试探究
轴的垂轴弦,其它条件不变,试探究![]() 是否为定值?(不需要证明);请你给出双曲线
是否为定值?(不需要证明);请你给出双曲线![]() 中相类似的结论,并证明你的结论。
中相类似的结论,并证明你的结论。
一、1. 2.3 3.
2.3 3. 4.18 5.
4.18 5. 6.55 7.
6.55 7. 8.0 9.7 10.0或-2
8.0 9.7 10.0或-2
11. 12.
12.
二、13.C 14.B 15.D 16.A
三、17.解:(1) ;
;
(2) ;
;
(3)表面积S=48.
18.解:(1)  ,
,

(2)
由 ,得当
,得当 时,
时, 取得最小值-2
取得最小值-2
19.解:(1)

(2)
 ,①
,①
 ,②
,②
②-①,整理,得
20.解:(1) ,设
,设
则
任取 ,
, ,
,
当 时,
时, 单调递减;
单调递减;
当 时,
时, 单调递增.
单调递增.
由 得
得
 的值域为
的值域为 .
.
(2)设 ,
,
则 ,
,
所以 单调递减.
单调递减.
(3)由 的值域为:
的值域为:
所以满足题设仅需:
解得, .
.
21.解:(1)
又
(2) 应用第(1)小题结论,得
应用第(1)小题结论,得 取倒数,得
取倒数,得
(3)由正弦定理,原题⇔△ABC中,求证:
证明:由(2)的结论得, 且
且 均小于1,
均小于1,
 ,
,

(4)如得出:四边形ABCD中,求证: 且证明正确给3分;
且证明正确给3分;
如得出:凸n边形A 求证:
求证:
 且证明正确给4分.
且证明正确给4分.
如能应用到其它内容有创意则给高分.
如得出: 为各项为正数的等差数列,
为各项为正数的等差数列, ,求证:
,求证:
 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com