练习册

  • 练习册
  • 试题
    C．当时.在x轴上 D．当时.在y轴上 【查看更多】

     

    题目列表(包括答案和解析)

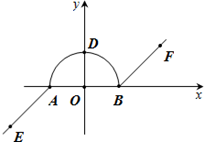    精英家教网如图，在平面直角坐标系xOy中，我把由两条射线AE，BF和以AB为直径的半圆所组成的图形叫作图形C（注：不含AB线段）．已知A（-1，0），B（1，0），AE∥BF，且半圆与y轴的交点D在射线AE的反向延长线上．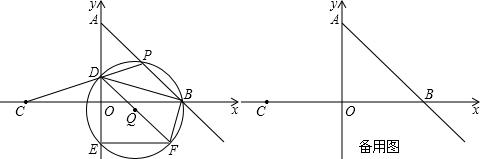
    （1）求两条射线AE，BF所在直线的距离；
    （2）当一次函数y=x+b的图象与图形C恰好只有一个公共点时，写出b的取值范围；当一次函数y=x+b的图象与图形C恰好只有两个公共点时，写出b的取值范围．

    查看答案和解析>>

    如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（0，4），点B的坐标为（4，0），点C的坐标为（-4，0），点P在射线AB上运动，连结CP与y轴交于点D，连结BD．过P，D，B三点作⊙Q与y轴的另一个交点为E，延长DQ交⊙Q于点F，连结EF，BF．

    （1）求直线AB的函数解析式；
    （2）当点P在线段AB（不包括A，B两点）上时．
    ①求证：∠BDE=∠ADP；
    ②设DE=x，DF=y．请求出y关于x的函数解析式；
    （3）请你探究：点P在运动过程中，是否存在以B，D，F为顶点的直角三角形，满足两条直角边之比为2：1？如果存在，求出此时点P的坐标：如果不存在，请说明理由．

    查看答案和解析>>

    如图，在平面直角坐标系xOy中，圆C：(x＋1)2＋y2＝16，点F(1，0)，E是圆C上的一个动点，EF的垂直平分线PQ与CE交于点B，与EF交于点D.

    (1)求点B的轨迹方程；
    (2)当点D位于y轴的正半轴上时，求直线PQ的方程；
    (3)若G是圆C上的另一个动点，且满足FG⊥FE，记线段EG的中点为M，试判断线段OM的长度是否为定值？若是，求出该定值；若不是，说明理由．

    查看答案和解析>>

    如图，在空间直角坐标系中，已知直三棱柱的顶点A在x轴上，AB平行于y轴，侧棱AA1平行于z轴．当顶点C在y轴正半轴上运动时，以下关于此直三棱柱三视图的表述正确的是（　　）
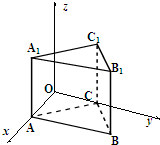
    A．该三棱柱主视图的投影不发生变化
    B．该三棱柱左视图的投影不发生变化
    C．该三棱柱俯视图的投影不发生变化
    D．该三棱柱三个视图的投影都不发生变化
    精英家教网

    查看答案和解析>>

    如图，在平面直角坐标系xoy中，圆C：（x+1）2+y2=16，点F（1，0），E是圆C上的一个动点，EF的垂直平分线PQ与CE交于点B，与EF交于点D．
    （1）求点B的轨迹方程；
    （2）当D位于y轴的正半轴上时，求直线PQ的方程；
    （3）若G是圆上的另一个动点，且满足FG⊥FE．记线段EG的中点为M，试判断线段OM的长度是否为定值？若是，求出该定值；若不是，说明理由．

    查看答案和解析>>

    一、选择题（每题5分，共60分）

    1―5 ACCBA  6―10 BCABD  11―12 DB

    2,4,6

    13．   14．   15．   16．①②③

    三、解答题（17―21题每小题12分，22题14分，共74分）

    17．解：（Ⅰ）

    （Ⅱ）

    又

    当且仅当时，△ABC面积取最大值，最大值为.

    18．解：（Ⅰ）依题意得

    （Ⅱ）

    又

    19．解法一：（Ⅰ）平面ACE.   

    ∵二面角D―AB―E为直二面角，且， 平面ABE.

    （Ⅱ）连结BD交AC于C，连结FG，

    ∵正方形ABCD边长为2，∴BG⊥AC，BG=，

    平面ACE，

    （Ⅲ）过点E作交AB于点O. OE=1.

    ∵二面角D―AB―E为直二面角，∴EO⊥平面ABCD.

    设D到平面ACE的距离为h，

    平面BCE， 

    解法二：（Ⅰ）同解法一.

    （Ⅱ）以线段AB的中点为原点O，OE所在直

    线为x轴，AB所在直线为y轴，过O点平行

    于AD的直线为z轴，建立空间直角坐标系

    O―xyz，如图.

    面BCE，BE面BCE， ，

    在的中点，

     设平面AEC的一个法向量为，

    则解得

           令得是平面AEC的一个法向量.

           又平面BAC的一个法向量为，

           ∴二面角B―AC―E的大小为

    （III）∵AD//z轴，AD=2，∴，

    ∴点D到平面ACE的距离

    20．解：（1）

    ；

    （2）

    ，,

    ，有最大值；即每年建造12艘船，年利润最大（8分）

    （3），（11分）

    所以，当时，单调递减，所以单调区间是，且

    21．解：(I)∵，且，

    ∴①④

    又由在处取得极小值－2可知②且③

    将①②③式联立得∴。   (4分)

    由得同理由得

    ∴的单调递减区间是[-1,1], 单调递增区间是(-∞,1和   (6分)

    (II)由上问知：,∴。

    又∵。∴。∴。∴

    ∵，∴>0。∴。(8分)

    ∴当时，的解集是，

    显然A不成立，不满足题意。

    ∴，且的解集是。   (10分)

    又由A知。解得。(12分)

    22．解：（1）设M(x，y)是所求曲线上的任意一点，P（x1，y1）是方程x2 +y2 =4的圆上的任意一点，则

        则有：得，

        轨迹C的方程为

       （1）当直线l的斜率不存在时，与椭圆无交点.

        所以设直线l的方程为y = k(x+2)，与椭圆交于A(x1，y1)、B(x2，y2)两点，N点所在直线方程为

        由

        由△=

        即 …   

        即，∴四边形OANB为平行四边形

        假设存在矩形OANB，则，即，

        即，

        于是有    得 … 设，

    即点N在直线上.

     ∴存在直线l使四边形OANB为矩形，直线l的方程为

     

     

     

     


    同步练习册答案