
题目列表(包括答案和解析)
 上的1级类增函数
上的1级类增函数 上的
上的 级类增函数,则实数a的最小值为2
级类增函数,则实数a的最小值为2 上的1级类增函数
上的1级类增函数 上的
上的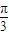 级类增函数,则实数a的最小值为2
级类增函数,则实数a的最小值为2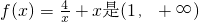 上的1级类增函数
上的1级类增函数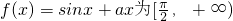 上的
上的 级类增函数,则实数a的最小值为2
级类增函数,则实数a的最小值为2| 1 | 2 |
1.C 2.C 3.D 4.A 5.D 6.D 7.B 8.D 9.B 10.C
l1.A 12.A
13.
14.15
15.
16.(1,2)
提示:
1.C 
2.C  .
.
3.D 
4.A 直线与圆相切 .
.
5.D 由 得
得 ,极坐标为(
,极坐标为( ,
, ).
).
6.D 将 的图象向右平移
的图象向右平移 个单位,再向下平移一个单位,
个单位,再向下平移一个单位, ?
?
7.B 该几何体是上面是正四棱锥,下面为正方体,
 体积为
体积为 .
.
8.D  .
.
9.B 画出平面区域 则
则 到
到
直线 的最大距离为
的最大距离为
10.C 
 ,
, ,
,
 ,
, .
.
11.A  ,设
,设 ,
,
则d方程为 .
.
 过点
过点 ,
,




12.A  的值域为
的值域为
 (或由
(或由 )
)

(当且仅当 )
)
13. .
.
 ,
,  .
.
14.15  ;
;
 ;
;  .
.
15.
16.(1,2) 
17.解:(1) , (2分)
, (2分)
 . (4分)
. (4分)
由余弦定理,得 . (6分)
. (6分)
(2) , (7分)
, (7分)
 (9分)
(9分)  (10分)
(10分)
 (11分)
(11分)
 (11分)
(11分)
 (12分)
(12分)
18.解:记基本事件为( ,
, ),
),
则有(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),
(2,5),(2,6),(3,1),(3,2),(3,3).(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),
(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),
(6,3),(6,4),(6,5),(6,6).共36个基本事件. (2分)
其中满是 的基本事件有
的基本事件有
(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4), (2,5),(2,6),(3,4),
(3,5),(3,6),(4,5),(4,6),(5,6), 共15个. (5分)
满足 的基本事件有
的基本事件有
(1,5),(1,6),(2,4),(2,5),(2,6),(3,3),(3,4),(3,5),(3,6),(4,2),(4,3).
(4,4),(4,5),(5,1),(5,2),(5,3),(5,4),(6,1),(6,2),(6,3),共20个.(8分)
∴(1) 的概率
的概率 (10分)
(10分)
(2) 的概率
的概率 (考虑反面做也可) (12分)
(考虑反面做也可) (12分)
 l9.(1)证明:如图,连结
l9.(1)证明:如图,连结 .
.
∵四边形 为矩形且F是
为矩形且F是 的中点.
的中点.
∴ 也是
也是 的中点. (1分)
的中点. (1分)
又E是 的中点,
的中点, (2分)
(2分)
∵EF 由
由 面
面 面
面 .(4分)
.(4分)
(2)证明:∵面 面
面 ,面
,面 面
面 ,
,
 .
.
又 面
面 (6分)
(6分)
又 是相交直线,
是相交直线, 面
面 (7分)
(7分)
又 面
面 面
面 面
面 . (8分)
. (8分)
(3)解:取 中点为
中点为 .连结
.连结
∵面 面
面 及
及 为等腰直角三角形,
为等腰直角三角形, 面
面 ,即
,即 为四棱锥
为四棱锥 的高. (10分)
的高. (10分)
 .
.
又 .∴四棱锥
.∴四棱锥 的体积
的体积 (12分)
(12分)
20.解:(1)由题意,得
 (3分)
(3分)
∴椭圆 的方程为
的方程为 (4分)
(4分)
(2)若直线 将圆
将圆 分割成弧长的比值为
分割成弧长的比值为 的两段圆弧,
的两段圆弧,
则其中劣弧所对的圆心角为120°. (6分)
又圆 的圆心在直线
的圆心在直线 上,点
上,点 是圆
是圆 与直线
与直线 的交点,
的交点,
设Q是 与圆
与圆 的另一交点,则
的另一交点,则 . (7分)
. (7分)
由①知 (8分)
(8分)
设直线 的倾斜角为
的倾斜角为 ,则
,则 或
或 (9分)
(9分)
 (10分)
(10分)
或 (11分)
(11分)
∴直线 的方程为
的方程为 或
或 (12分)
(12分)
21.(1)解: 成等比数列,
成等比数列, ,即
,即 .
.
又 (3分)
(3分)
 (5分)
(5分)
(2)证明: , (6分)
, (6分)

 (7分)
(7分)


 (当且仅当
(当且仅当 时取“=”). ① (9分)
时取“=”). ① (9分)

(当值仅当 即
即 时取“=”) ② (11分)
时取“=”) ② (11分)
又①②中等号不可能同时取到, .(12分)
.(12分)
22.(1)解:∵函数 在
在 时取得一个极值,且
时取得一个极值,且 ,
,
 ,
,
 (2分)
(2分)
 .
.
 或
或 时,
时, 或
或 时,
时, 时,
时,
 , (4分)
, (4分)
 在
在 上都是增函数,在
上都是增函数,在 上是减函数. (5分)
上是减函数. (5分)
∴使 在区间
在区间 上是单调函数的
上是单调函数的 的取值范围是
的取值范围是 (6分)
(6分)
(2)由(1)知 .
.
设切点为 ,则切线的斜率
,则切线的斜率 ,所以切线方程为:
,所以切线方程为:
 . (7分)
. (7分)
将点 代人上述方程,整理得:
代人上述方程,整理得: . (9分)
. (9分)
∵经过点 可作曲线
可作曲线 的三条切线,
的三条切线,
∴方程 有三个不同的实根. (11分)
有三个不同的实根. (11分)
设 ,则
,则
 ,
,
 在
在 上单调递增,在
上单调递增,在 上单调递减,在
上单调递减,在 上单调递增,(12分)
上单调递增,(12分)
故 (13分)
(13分)
解得: . (14分)
. (14分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com