由此得.化简得——青夏教育精英家教网—

由此得.化简得【查看更多】

探究函数的最小值，并确定取得最小值时x的值，列表如下：

x	…	0.5	1	1.5	1.7	1.9	2	2.1	2.2	2.3	3	4	5	7	…
y	…	8.5	5	4.17	4.05	4.005	4	4.005	4.002	4.04	4.3	5	5.8	7.57	…

请观察表中y值随x值变化的特点，完成以下问题：

（1）函数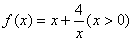在区间上递增.

当时，y_最小 = .

（2）函数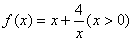在区间上递减，并用定义证明之；

（3）函数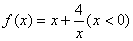时，有最值吗？是最大值还是最小值？此时x为何值？

（写出结果，简要说明理由）

某个计算机有A，B两个数据输入口，另有C是计算结果的输出口，计算过程是由A，B分别输入正整数m和n．经计算得正整数k，然后由C输出(过程可简单表示为关系式f(m，n)＝k)．此种计算装置完成的计算机满足以下三个性质．

①若A，B的输入1，则输出的结果为2，即f(1，1)＝2；

②若A输入1，B的输入由n变为n＋1，则输出的结果比原来增大2，即f(1，n＋1)＝f(1，n)＋2；

③若B输入n，A的输入由m变为m＋1，则输出结果为原来的3倍，即f(m＋1，n)＝3f(m，n)．

试回答下列问题：

(1)若A输入2，B输入3，则输出结果为多少？

(2)若A输入1，B输入n(n∈N₊)，则输出结果为多少？

(3)由C能输出多少个不同的两位数？

说明：本题题干比较长，情景相对陌生，将题干中的语言转化为数列语言是解题关键．

[1]函数f（x）=x³+ax²+3x-9，已知f（x）在x=-3时取得极值，则a=______．
[2]观察下列等式：1=1，1-4=-（1+2），1-4+9=（1+2+3），1-4+9-16=-（1+2+3+4），…由此推测第n个等式为______．（不必化简结果）

[1]函数f（x）=x³+ax²+3x-9，已知f（x）在x=-3时取得极值，则a= ．
[2]观察下列等式：1=1，1-4=-（1+2），1-4+9=（1+2+3），1-4+9-16=-（1+2+3+4），…由此推测第n个等式为．（不必化简结果）

6、[1]函数f（x）=x³+ax²+3x-9，已知f（x）在x=-3时取得极值，则a=

5

．
[2]观察下列等式：1=1，1-4=-（1+2），1-4+9=（1+2+3），1-4+9-16=-（1+2+3+4），…由此推测第n个等式为

1-4+9-16+…+（-1）ⁿ⁺¹n²=（-1）ⁿ⁺¹（1+2+3+…+n）

．（不必化简结果）