
题目列表(包括答案和解析)
袋子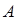 和
和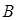 中装有若干个均匀的红球和白球,从
中装有若干个均匀的红球和白球,从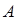 中摸一个红球的概率是
中摸一个红球的概率是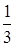 ,从
,从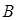 中摸出一个红球的概率为
中摸出一个红球的概率为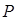 .
.
⑴从A中有放回地摸球,每次摸出一个,有3次摸到红球则停止.
① 求恰好摸5次停止的概率;
② 记5次之内(含5次)摸到红球的次数为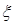 ,求随机变量
,求随机变量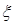 的分布列及数学期望
的分布列及数学期望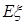 .
.
⑵若A、B两个袋子中的球数之比为1:2,将A、B中的球装在一起后,从中摸出一个红球的概率是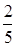 ,求
,求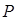 的值.
的值.
 .从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止.
.从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止. .从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止.
.从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止.袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是![]() ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.
(Ⅰ) 从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止.
(i)求恰好摸5次停止的概率;
(ii)记5次之内(含5次)摸到红球的次数为![]() ,求随机变量
,求随机变量![]() 的分布率及数学期望E
的分布率及数学期望E![]() .
.
(Ⅱ) 若A、B两个袋子中的球数之比为12,将A、B中的球装在一起后,从中摸出一个红球的概率是![]() ,求p的值.
,求p的值.
(Ⅰ) 从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止.(i)求恰好摸5次停止的概率;(ii)记5次之内(含5次)摸到红球的次数为![]() ,求随机变量
,求随机变量![]() 的分布率及数学期望E
的分布率及数学期望E![]() .
.
(Ⅱ) 若A、B两个袋子中的球数之比为1:2,将A、B中的球装在一起后,从中摸出一个红球的概率是![]() ,求p的值.
,求p的值.
一、选择题: BBDBA BBBCB AC
二、填空题: 13.6
14. 15.1 16. ②③
15.1 16. ②③
三.解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.
解:(1)∵  , 且与向量
, 且与向量 所成角为
所成角为
∴  , ∴
, ∴  ,
,
又 ,∴
,∴  ,即
,即 。
。
(2)由(1)可得:
∴ 



∵  ,
,
∴  ,
,
∴  ,
,
∴ 当 =1时,A=
=1时,A=
∴AB=2,
则
18.解:(1)P=
(2)随机变量 的取值为0, 1, 2, 3.
的取值为0, 1, 2, 3.
由n次独立重复试验概率公式 得
得




随机变量 的分布列是
的分布列是

0
1
2
3





 的数学期望是
的数学期望是 
19.证明(Ⅰ)

 AB∥DC,
AB∥DC, DC
DC 平面PAD.
平面PAD.
 DC
DC PD
DC
PD
DC AD,
AD,
 PDA为二面角P-CD-B的平面角.
PDA为二面角P-CD-B的平面角.
故 PDA=45°
PDA=45°  PA=AD=3,
PA=AD=3,

 APD=45°.
APD=45°.  PA
PA AD.
AD.
 又PA
又PA AB ,
AB , PA
PA 平面ABCD.
平面ABCD.
(Ⅱ)证法一:延长DA,CE交于点N,连结PN,
由折叠知 又
又 .
.
 ,
,
又由(1)知 ,
,
 为二面角
为二面角 的平面角.………9分
的平面角.………9分
在直角三角形 中,
中,
 ,
, .
.
即平面PEC和平面PAD所成锐二面角为30°.
证法二:如图建立空间直角坐标系 ,
,
则

 ,
,
设 为平面
为平面 的法向量,则
的法向量,则
 ,可设
,可设 ,又平面
,又平面 的法向量
的法向量 ,
,
 .
.
 .
.
20.解:(I)依题意得


(II)依题意得, 上恰有两个相异实根,
上恰有两个相异实根,
令

故 在[0,1]上是减函数,在
在[0,1]上是减函数,在 上是增函数,
上是增函数,


21.解:(1)直线 方程为
方程为 与
与 联立得
联立得

(2)设弦AB的中点M的坐标为 依题意有
依题意有



所以弦AB的中点M的轨迹是以 为中心,
为中心,
焦点在 轴上,长轴长为1,短轴长为
轴上,长轴长为1,短轴长为 的椭圆。
的椭圆。
(3)设直线AB的方程为
代入 整理得
整理得
 直线AB过椭圆的左焦点F,
直线AB过椭圆的左焦点F, 方程有两个不等实根。
方程有两个不等实根。
记 中点
中点
则
 的垂直平分线NG的方程为
的垂直平分线NG的方程为
令 得
得

 点G横坐标的取值范围为
点G横坐标的取值范围为
22.解:(I)把
(II) , ①
, ①
 ②
②
①式减②式得, , 变形得
, 变形得 ,
,
又因为 时上式也成立。
时上式也成立。
所以,数列 为公比的等比数列,
为公比的等比数列,
所以
(III) ,
,


 所以
所以
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com