
题目列表(包括答案和解析)
给出下列四个命题:
①若直线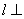 平面
平面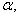
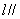 平面
平面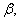 则
则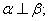
②若平面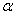 内有不共线的三点到平面
内有不共线的三点到平面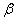 的距离相等,则
的距离相等,则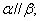
③若一个二面角的两个半平面所在的平面分别垂直于另一个二面角的两个半平面所在的平面,则这两个二面角的平面角互为补角;
④过空间中任意一点一定可以作一个和两条异面直线都平行的平面.
其中正确命题的个数有( )
A.1 B.2 C.3 D.4
二面角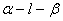 的平面角为120°,在面
的平面角为120°,在面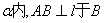 ,AB=2在平面β内,CD⊥ l于D,CD=3,BD=1,M是棱l上的一个动点,则AM+CM的最小值为 ( )
,AB=2在平面β内,CD⊥ l于D,CD=3,BD=1,M是棱l上的一个动点,则AM+CM的最小值为 ( )
A.6 B.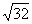 C.
C.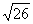 D.5
D.5
 如图,在等腰梯形ABCD中,AB∥DC,AB = 4,CD = 2,等腰梯形的高为3,O为AB中点,PO⊥平面ABCD,垂足为O,PO = 2,EA∥PO.
如图,在等腰梯形ABCD中,AB∥DC,AB = 4,CD = 2,等腰梯形的高为3,O为AB中点,PO⊥平面ABCD,垂足为O,PO = 2,EA∥PO.
(1)求证:BD⊥平面EAC;
(2)求二面角E—AC—P的平面角的余弦值.
必做题, 本小题10分.解答时应写出文字说明、证明过程或演算步骤.
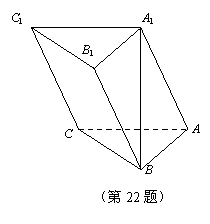
如图,在三棱柱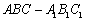 中,
中,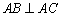 ,顶点
,顶点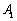 在底面
在底面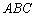 上的射影恰为点B,且
上的射影恰为点B,且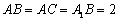 .
.
(1)求棱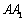 与BC所成的角的大小;
与BC所成的角的大小;
 (2)在棱
(2)在棱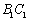 上确定一点P,使
上确定一点P,使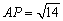 ,并求出二面角
,并求出二面角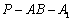 的平面角的余弦值.
的平面角的余弦值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com