
题目列表(包括答案和解析)
借助计算器,用二分法求出![]() 在区间
在区间![]() 内的近似解(精确到
内的近似解(精确到![]() )
)
(本小题12分) 适当饮用葡萄酒可以预防心脏病,下表中的信息是19个发达国家一年中平均每人喝葡萄酒摄取酒精的升数z以及一年中每10万人因心脏病死亡的人数,
|
国家 |
澳大利亚 |
奥地利 |
比利时 |
加拿大 |
丹麦 |
芬兰 |
法国 |
冰岛 |
爰尔兰 |
意大利 |
|
x |
2.5 |
3.9 |
2.9 |
2.4 |
2.9 |
0.8 |
9.1 |
0.8 |
0.7 |
7.9 |
|
y |
211 |
167 |
131 |
191 |
220 |
297 |
71 |
221 |
300 |
107 |
|
国家 |
荷兰 |
新西兰 |
挪威 |
西班牙 |
瑞典 |
瑞士 |
英国 |
美国 |
德国 |
|
x |
1.8 |
1.9 |
0.8 |
6.5 |
1.6 |
5.8 |
1.3 |
1.2 |
2.7 |
|
y |
167 |
266 |
227 |
86 |
207 |
115 |
285 |
199 |
172 |
(1)画出散点图,说明相关关系的方向、形式及强度;
(2)求出每10万人中心脏病死亡人数,与平均每人从葡萄酒得到的酒精x(L)之间的线性回归方程.
(3)用(2)中求出的方程来预测以下两个国家的心脏病死亡率,其中一个国家的成人每年平均从葡萄酒中摄取1L的酒精,另一国则是8 L.
活动:学生审题,思考并交流,探讨解题的思路,教师及时提示引导,因两圆的交点坐标同时满足两个圆方程,联立方程组,消去x2项、y2项,即得两圆的两个交点所在的直线方程,利用勾股定理可求出两圆公共弦长.
某种型号的汽车在匀速行驶中每小时耗油量 关于行驶速度
关于行驶速度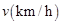 的函数解析式可以表示为:
的函数解析式可以表示为: .已知甲、乙两地相距
.已知甲、乙两地相距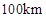 ,设汽车的行驶速度为
,设汽车的行驶速度为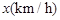 ,从甲地到乙地所需时间为
,从甲地到乙地所需时间为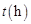 ,耗油量为
,耗油量为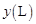 .
.
(1)求函数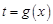 及
及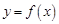 ;
;
(2)求当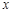 为多少时,
为多少时,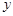 取得最小值,并求出这个最小值.
取得最小值,并求出这个最小值.
【解析】(1) 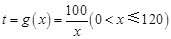 ,根据
,根据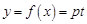 可求出y=f(x).
可求出y=f(x).
(2)求导,根据导数确定其最小值.
在△ABC中,角A,B,C所对边分别为a,b,c,且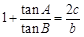 .
.
(Ⅰ)求角A;
(Ⅱ)若m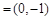 ,n
,n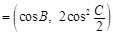 ,试求|m
,试求|m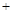 n|的最小值.
n|的最小值.
【解析】(I)把切化成弦,然后根据正弦定理,把等号右边的边的比,转化为对应的角的正弦的比,再借助诱导公式求A.
(II)根据第(I)问求出的A角,然后把C角用B角来表示,再借助向量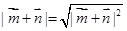 表示成关于角B的函数,然后根据三角函数的知识求最小值即可.
表示成关于角B的函数,然后根据三角函数的知识求最小值即可.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com