
题目列表(包括答案和解析)
| 学生的编号 | 1 | 2 | 3 | 4 | 5 |
| 数学成绩xi | 80 | 75 | 70 | 65 | 60 |
| 物理成绩yi | 70 | 66 | 68 | 64 | 62 |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
| x | 2 i |
| 学生的编号i | 1 | 2 | 3 | 4 | 5 |
| 数学xi | 80 | 75 | 70 | 65 | 60 |
| 物理yi | 70 | 66 | 68 | 64 | 62 |
| ? |
| y |
| |||||||
|
. |
| y |
. |
| x |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
| x | 2 i |
| 5 |
 |
| i=1 |
| ? |
| y |
(本题满分15分)杨辉是中国南宋末年的一位杰出的数学家、数学教育家,杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律.下图是一个11阶杨辉三角:
(1)求第20行中从左到右的第3个数;
(2)若第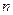 行中从左到右第13与第14个数的比为
行中从左到右第13与第14个数的比为 ,求
,求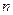 的值;
的值;
(3)写出第 行所有数的和,写出
行所有数的和,写出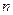 阶(包括
阶(包括 阶)杨辉三角中的所有数的和;
阶)杨辉三角中的所有数的和;
(4)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35,我们发现 ,事实上,一般地有这样的结论:第
,事实上,一般地有这样的结论:第 斜列中(从右上到左下)前
斜列中(从右上到左下)前 个数之和,一定等于第
个数之和,一定等于第 斜列中第
斜列中第 个数.
个数.
试用含有 ,
,
 的数学式子表示上述结论,并证明.
的数学式子表示上述结论,并证明.
(本题满分15分)杨辉是中国南宋末年的一位杰出的数学家、数学教育家,杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律.下图是一个11阶杨辉三角:

(1)求第20行中从左到右的第3个数;
(2)若第 行中从左到右第13与第14个数的比为
行中从左到右第13与第14个数的比为 ,求
,求 的值;
的值;
(3)写出第 行所有数的和,写出
行所有数的和,写出 阶(包括
阶(包括 阶)杨辉三角中的所有数的和;
阶)杨辉三角中的所有数的和;
(4)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35,我们发现 ,事实上,一般地有这样的结论:第
,事实上,一般地有这样的结论:第 斜列中(从右上到左下)前
斜列中(从右上到左下)前 个数之和,一定等于第
个数之和,一定等于第 斜列中第
斜列中第 个数.
个数.
试用含有 ,
,
 的数学式子表示上述结论,并证明.
的数学式子表示上述结论,并证明.
已知某校5个学生的数学和物理成绩如下表

(1)假设在对这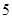 名学生成绩进行统计时,把这
名学生成绩进行统计时,把这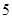 名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有
名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有 名学生的物理成绩是自己的实际分数的概率是多少?
名学生的物理成绩是自己的实际分数的概率是多少?
(2)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系的,在上述表格是正确的前提下,用 表示数学成绩,用
表示数学成绩,用 表示物理成绩,求
表示物理成绩,求 与
与 的回归方程;
的回归方程;
(3)利用残差分析回归方程的拟合效果,若残差和在 范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.
范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.
参考数据和公式: ,其中
,其中 ,
, ;
;
 ,残差和公式为:
,残差和公式为:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com