
题目列表(包括答案和解析)
由下面四个图形中的点数分别给出了四个数列的前四项,将每个图形的层数增加可得到这四个数列的后继项.按图中多边形的边数依次称这些数列为“三角形数列”、“四边形数列”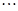 ,将构图边数增加到
,将构图边数增加到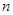 可得到“
可得到“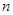 边形数列”,记它的第
边形数列”,记它的第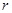 项为
项为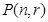 ,
,
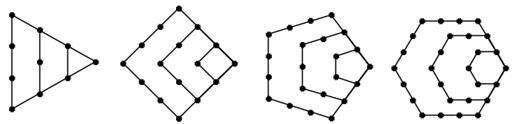
1,3,6,10 1,4,9,16 1,5,12,22 1,6,15,28
(1)
求使得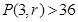 的最小
的最小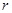 的取值;
的取值;
(2)
试推导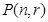 关于
关于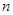 、
、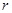 的解析式;
的解析式;
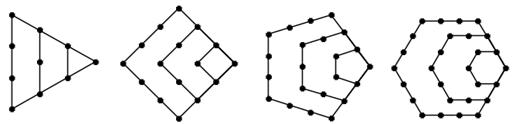
( 3) 是否存在这样的“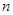 边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.
边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.
 ,将构图边数增加到
,将构图边数增加到 可得到“
可得到“ 边形数列”,记它的第
边形数列”,记它的第 项为
项为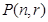 ,
,
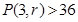 的最小
的最小 的取值;
的取值;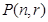 关于
关于 、
、 的解析式;
的解析式; 边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.
边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.在平面直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为
 点
点 是曲线
是曲线 上的动点.
上的动点.
(1)求线段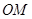 的中点
的中点 的轨迹的直角坐标方程;
的轨迹的直角坐标方程;
(2) 以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,若直线
轴的正半轴为极轴建立极坐标系,若直线 的极坐标方程为
的极坐标方程为 ,求点
,求点 到直线
到直线 距离的最大值.
距离的最大值.
【解析】第一问利用设曲线 上动点
上动点 ,由中点坐标公式可得
,由中点坐标公式可得
 所以点
所以点 的轨迹的参数方程为
的轨迹的参数方程为
 消参可得
消参可得
第二问,由题可知直线 的直角坐标方程为
的直角坐标方程为 ,因为原点到直线的距离为
,因为原点到直线的距离为 ,
,
所以点 到直线的最大距离为
到直线的最大距离为
某食品厂定期购买面粉,已知该厂每天需用面粉6吨,每吨面粉的价格为1800元,面粉的保管等其它费用为平均每吨每天3元,购面粉每次支付运费900元.
(1)求该厂多少天购买一次面粉,才能使每天支付的总费用最少?
(2)若提供面粉的公司规定:当一次购买面粉不少于210吨时,其价格可享受9折优惠(即原价的90%)问该厂是否考虑利用此优惠条件?请说明理由.
设平面向量![]() (其中
(其中![]() ),且
),且![]() .
.
(1)求函数y=f(x)的表达式;
(2)若函数y=f(x)对任意![]() 都有(x1-x2)[f(x1)-f(x2)]>0,求此时
都有(x1-x2)[f(x1)-f(x2)]>0,求此时![]() 在[1,+∞]上的最小值;
在[1,+∞]上的最小值;
(3)若点(x0,f(x0))在不等式![]() 所表示的区域内,且x0为方程
所表示的区域内,且x0为方程![]() 的一个解,当k<4时,请判断x0是否为方程f(x)=x的根,并说明理由.
的一个解,当k<4时,请判断x0是否为方程f(x)=x的根,并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com