题目列表(包括答案和解析)
C．选修4—4：坐标系与参数方程
(本小题满分10分)
在极坐标系中，圆
的方程为
，以极点为坐标原点，极轴为
轴的正半轴建立平面直角坐标系，直线
的参数方程为
（
为参数），判断直线和圆的位置关系．
C．选修4-4：坐标系与参数方程（本小题满分10分）
在平面直角坐标系
中，求过椭圆
（
为参数）的右焦点且与直线
（
为参数）平行的直线的普通方程。
C．（选修4—4：坐标系与参数方程）
在极坐标系中，圆
的方程为
，以极点为坐标原点，极轴为
轴的正
半轴建立平面直角坐标系，直线
的参数方程为
（
为参数），求直线被
截
得的弦
的长度.
C．（坐标系与参数方程选做题）已知极坐标的极点在直角坐标系的原点O处，极轴与x轴的正半轴重合，曲线C的参数方程为
（
为参数），直线l的极坐标方程为
．点P在曲线C上，则点P到直线l的距离的最小值为
．
C．选修4－4：坐标系与参数方程
在直角坐标系
中，已知曲线
的参数方程是
（
是参数），若以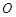
为极点，
轴的正半轴为极轴，取与直角坐标系中相同的单位长度，建立极坐标系，求曲线的极坐标方程．
一、选择题：
1．A 2． D 3．C 4．A 5．D 6．A 7．B 8．B 9．C 10．C
二、填空题：
11．
12．100 13．2 14．
15．
16．276
三、解答题：
17．解：
（I）
----2分
-------------3分
函数
的最小正周期是
-------------4分
18．解：（Ⅰ）由已知得，
则
． -------------4分
（Ⅱ）中国乒乓球队获得金牌数是一随机变量
，
它的所有可能取值为0，1，2，3，4 （单位: 枚）．那么-------------5分
-------------6分
，
-------------8分
19．解：
（I）
是矩形，
--------------1分
又
-------------2分
-------------3分
CD
----------4分
（II）由
，及（I）结论可知DA、DC、DS
两两互相垂直，
建立如图所示的空间直角坐标系
--------------5分
--------------6分
--------------7分
AD与SB所成的角的余弦为
--------------8分
（III）
设面SBD的一个法向量为
--------------9分
CD是CS在面ABCD内的射影，且
--------------6分
--------------8分
从而SB与AD的成的角的余弦为
（III）
面ABCD．
BD为面SDB与面ABCD的交线．
SDB
于F，连接EF， 从而得：
为二面角A―SB―D的平面角
--------------10分
在矩形ABCD中，对角线
中，
所以所求的二面角的余弦为
--------------12分
20．解：
（Ⅰ）由
----------1分
----------2分
------------3分
（Ⅱ）假设存在实数t，使得
为等差数列．
则
------------4分
------------5分
------------6分
存在t=1，使得数列
为等差数列． ------------7分
（Ⅲ）由（1）、（2）知：
------------8分
又为等差数列．
------------9分
------------10分
--11分
………………12分
21．解：
|
…………2分
………………3分
，
，椭圆C的方程为
--4分
，
， 
时，
， ----５分
---------６分
，则
（舍去），
------------７分
．
------------8分
=6
．--９分
………………12分
……………………13分
…………14分
．
时，
，
．
，解得
．
时，
；当
时，
．
，
，无极大值 ． ………………（3分）
． 
． ………………（4分）
，令
，
时，
，
或
．
时，
．
时，得
，
；
．
，增区间
． 
时，
；增区间为
．
，
． …………………………（9分）
时，
对一切正整数成立。…………11分
（当且仅当n=1时取等号）
单调递增，
，
为正整数，得
，
满足条件．
的最大值为32． ………………………………（14分）