
题目列表(包括答案和解析)
(本小题共15分)已知函数 。
。
(1)若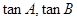 为方程
为方程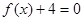 的两个实根,并且A,B为锐角,求m的取值范围;
的两个实根,并且A,B为锐角,求m的取值范围;
(2)对任意实数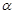 ,恒有
,恒有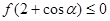 ,证明:
,证明: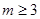 .
.
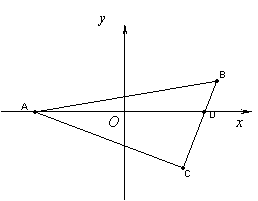
(本小题共15分)如图直角![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,椭圆
上,椭圆![]() 以
以![]() 为焦点且经过
为焦点且经过![]() .现以线段
.现以线段![]() 所在直线为
所在直线为![]() 轴,其中
轴,其中![]() 中点
中点![]() 为坐标原点建立直角坐标系.
为坐标原点建立直角坐标系.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 为椭圆
为椭圆![]() 内的一定点,点
内的一定点,点![]() 是椭圆上的一动点.求
是椭圆上的一动点.求![]() 的最值.
的最值.
 (3)设椭圆
(3)设椭圆![]() 分别与
分别与![]() 正半轴交于
正半轴交于![]() 两点,且
两点,且![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,求四边形
两点,求四边形![]() 面积的最大值.
面积的最大值.
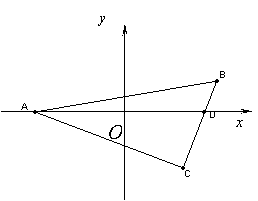
(本小题共15分)如图直角![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,椭圆
上,椭圆![]() 以
以![]() 为焦点且经过
为焦点且经过![]() .现以线段
.现以线段![]() 所在直线为
所在直线为![]() 轴,其中
轴,其中![]() 中点
中点![]() 为坐标原点建立直角坐标系.
为坐标原点建立直角坐标系.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 为椭圆
为椭圆![]() 内的一定点,点
内的一定点,点![]() 是椭圆上的一动点.求
是椭圆上的一动点.求![]() 的最值.
的最值.
 (3)设椭圆
(3)设椭圆![]() 分别与
分别与![]() 正半轴交于
正半轴交于![]() 两点,且
两点,且![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,求四边形
两点,求四边形![]() 面积的最大值.
面积的最大值.
(本小题共15分)如图直角![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,椭圆
上,椭圆![]() 以
以![]() 为焦点且经过
为焦点且经过![]() .现以线段
.现以线段![]() 所在直线为
所在直线为![]() 轴,其中
轴,其中![]() 中点
中点![]() 为坐标原点建立直角坐标系.
为坐标原点建立直角坐标系.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 为椭圆
为椭圆![]() 内的一定点,点
内的一定点,点![]() 是椭圆上的一动点.求
是椭圆上的一动点.求![]() 的最值.
的最值.
 (3)设椭圆
(3)设椭圆![]() 分别与
分别与![]() 正半轴交于
正半轴交于![]() 两点,且
两点,且![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,求四边形
两点,求四边形![]() 面积的最大值.
面积的最大值.
(本小题共12分)
现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
|
月收入(单位百元) |
[15,25 |
[25,35 |
[35,45 |
[45,55 |
[55,65 |
[65,75 |
|
频数 |
5 |
10 |
15 |
10 |
5 |
5 |
|
赞成人数 |
4 |
8 |
12 |
5 |
2 |
1 |
(1)由以上统计数据填下面2乘2列联表并问是否有99%的把握认为“月收入以5500为分界点对“楼市限购令” 的态度有差异;
|
|
月收入不低于55百元的人数 |
月收入低于55百元的人数 |
合计 |
|
赞成 |
|
|
|
|
不赞成 |
|
|
|
|
合计 |
|
|
|
(2)若对在[15,25)
,[25,35)的被调查中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为 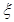 ,求随机变量
,求随机变量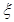 的分布列。
的分布列。
附: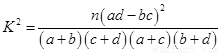
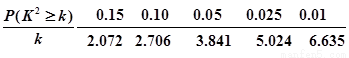
1. {2,8} 2.  3.
3.  4.
4. 
5. 
 6. 1 7.20
6. 1 7.20
8.  9.
9.  10.2
10.2
11. 12.
12.  13. [2,3] 14.
13. [2,3] 14. 
15.证明:(Ⅰ)在 中,
中,
∵ ,
, ,
, ,∴
,∴ .
.
∴ .????????????????? 2分
.????????????????? 2分
又 ∵平面 平面
平面 ,
,
平面 平面
平面 ,
, 平面
平面 ,
,
∴ 平面
平面 .
.
又 平面
平面 ,
,
∴平面 平面
平面 .………………………………………………………………4分
.………………………………………………………………4分
(Ⅱ)当 点位于线段PC靠近C点的三等分点处时,
点位于线段PC靠近C点的三等分点处时, 平面
平面 .………5分
.………5分
证明如下:连接AC,交 于点N,连接MN.
于点N,连接MN.
∵ ,所以四边形
,所以四边形 是梯形.
是梯形.
∵ ,∴
,∴ .
.
又 ∵ ,
,
∴
 ,∴
,∴ MN.…………………………………………………7分
MN.…………………………………………………7分
∵ 平面
平面 ,∴
,∴ 平面
平面 .………………………………………9分
.………………………………………9分
(Ⅲ)过 作
作 交
交 于
于 ,
,
∵平面 平面
平面 ,
,
∴ 平面
平面 .
.
即 为四棱锥
为四棱锥 的高.……………………………………………………11分
的高.……………………………………………………11分
又 ∵ 是边长为4的等边三角形,∴
是边长为4的等边三角形,∴ .……………12分
.……………12分
 在
在 中,斜边
中,斜边 边上的高为
边上的高为 ,此即为梯形
,此即为梯形 的高.
的高.
∴梯形 的面积
的面积 .
.
故 .……………………………………………14分
.……………………………………………14分
16.设 的二次项系数为
的二次项系数为 ,其图象上两点为(
,其图象上两点为( ,
, )、B(
)、B( ,
, )因为
)因为 ,
, ,所以
,所以 ,由x的任意性得f(x)的图象关于直线x=1对称, ………………………………………………………………(2分)
,由x的任意性得f(x)的图象关于直线x=1对称, ………………………………………………………………(2分)
∵  ,
, ,
, ,
,
 ,
, ,
,
 ,………………………………(4分)
,………………………………(4分)
∴ 当 时,∵f(x)在x≥1内是增函数,
时,∵f(x)在x≥1内是增函数,





 ,
, .
.
∵  , ∴
, ∴  .………………………………………………(8分)
.………………………………………………(8分)
当 时,∵f(x)在x≥1内是减函数.
时,∵f(x)在x≥1内是减函数.
同理可得 或
或 ,
, .………………………………………(11分)
.………………………………………(11分)
综上: 的解集是当
的解集是当 时,为
时,为
当 时,为
时,为 ,或
,或 .
.
17.解:(1)若 千米/小时,每小时耗油量为
千米/小时,每小时耗油量为 升/小时. 共耗油
升/小时. 共耗油 升.
升.
所以,从甲地到乙地要耗油
(2)设当汽车以 千米/小时的速度匀速行驶时耗油量最少,
千米/小时的速度匀速行驶时耗油量最少, ,耗油量为S升.
,耗油量为S升.
则 ,
,
 ,
,
令 ,解得,
,解得, .
.
列表:











单调减
极小值11.25
单调增

所以,当汽车以
18.解:(Ⅰ)设

对称轴方程 ,由题意
,由题意 或
或 或
或
∴ 或
或 或
或 ∴
∴
(Ⅱ)由已知与(Ⅰ)得: ,
, ,
,
 ,
, ,
, .
.
 椭圆的标准方程为
椭圆的标准方程为 .
.
设 ,
, ,联立
,联立
得 ,
,

又 ,
,
因为椭圆的右顶点为 ,
, ,即
,即 ,
,
 ,
,
 ,
, .
.
解得: ,
, ,且均满足
,且均满足 ,
,
当 时,
时, 的方程为
的方程为 ,直线过定点
,直线过定点 ,与已知矛盾;
,与已知矛盾;
当 时,
时, 的方程为
的方程为 ,直线过定点
,直线过定点 .
.
所以,直线 过定点,定点坐标为
过定点,定点坐标为 .
.
19. 解: (1) 由题知:  , 解得
, 解得 , 故
, 故 .
.
(2)  ,
,
 ,
,
 ,
,
又 满足上式. 所以
满足上式. 所以 .
.
(3) 若 是
是 与
与 的等差中项, 则
的等差中项, 则 ,
,
从而 , 得
, 得 .
.
因为 是
是 的减函数, 所以
的减函数, 所以
当 , 即
, 即 时,
时,  随
随 的增大而减小, 此时最小值为
的增大而减小, 此时最小值为 ;
;
当 , 即
, 即 时,
时,  随
随 的增大而增大, 此时最小值为
的增大而增大, 此时最小值为 .
.
又 , 所以
, 所以 ,
,
即数列 中
中 最小, 且
最小, 且 .
.
20. 解:(1)由题意得

而 ,所以
,所以 、
、 的关系为
的关系为
(2)由(1)知 ,
,

令 ,要使
,要使 在其定义域
在其定义域 内是单调函数,只需
内是单调函数,只需 在
在 内满足:
内满足: 恒成立.
恒成立.
①当 时,
时, ,因为
,因为 >
> ,所以
,所以 <0,
<0, <0,
<0,
∴ 在
在 内是单调递减函数,即
内是单调递减函数,即 适合题意;
适合题意;
②当 >0时,
>0时, ,其图像为开口向上的抛物线,对称轴为
,其图像为开口向上的抛物线,对称轴为 ,∴
,∴ ,
,
只需 ,即
,即 ,
,
∴ 在
在 内为单调递增函数,故
内为单调递增函数,故 适合题意.
适合题意.
③当 <0时,
<0时, ,其图像为开口向下的抛物线,对称轴为
,其图像为开口向下的抛物线,对称轴为 ,只要
,只要 ,即
,即 时,
时, 在
在 恒成立,故
恒成立,故 <0适合题意.
<0适合题意.
综上所述, 的取值范围为
的取值范围为 .
.
(3)∵ 在
在 上是减函数,
上是减函数,
∴ 时,
时, ;
; 时,
时, ,即
,即 ,
,
①当 时,由(2)知
时,由(2)知 在
在 上递减
上递减 <2,不合题意;
<2,不合题意;
②当0< <1时,由
<1时,由 ,
,
又由(2)知当 时,
时, 在
在 上是增函数,
上是增函数,
∴ <
< ,不合题意;
,不合题意;
③当 时,由(2)知
时,由(2)知 在
在 上是增函数,
上是增函数, <2,又
<2,又 在
在 上是减函数,
上是减函数,
故只需 >
> ,
, ,而
,而 ,
,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com