
题目列表(包括答案和解析)
(本题满分12分)有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表:
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 105 |
已知在全部105人中随机抽取1人为优秀的概率为![]() .
.
(Ⅰ)请完成上面的列联表;
(Ⅱ)从105名学生中选出10名学生组成参观团,若采用下面的方法选取:先用简单随机抽样从105人中剔除5人,剩下的100人再按系统抽样的方法抽取10人,请写出在105人 中,每人入选的概率(不必写过程).
(Ⅲ)把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀
的骰子,出现的点数之和作为被抽取人的序号,求“抽到6号或10号”的概率.
(本小题满分12分)某市调研考试后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的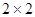 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为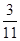 .
.
|
|
优秀 |
非优秀 |
合计 |
|
甲班 |
10 |
|
|
|
乙班 |
|
30 |
|
|
合计 |
|
|
110 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按99%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到9号或10号的概率.
附: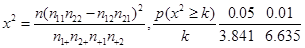 )
)
(本小题满分12分)某市调研考试后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的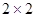 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为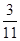 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 110 |
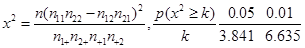 )
)(本小题满分12分)
某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图5所示,成绩不小于90分为及格.
| 甲 | 乙 | |
| 257 368 58 68 | 7 8 9 10 | 89 678 1235 1 |
(Ⅰ)甲班10名同学成绩的标准差 乙班10名同学成绩的标准差(填“>”,“<”);
(Ⅱ)从两班10名同学中各抽取一人,已知有人及格,求乙班同学不及格的概率;
(Ⅲ)从甲班10人中取一人,乙班10人中取两人,三人中及格人数记为X,
|
(本小题满分12分)
某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图5所示,成绩不小于90分为及格.
| 甲 | 乙 | |
| 257 368 58 68 | 7 8 9 10 | 89 678 1235 1 |
(Ⅰ)甲班10名同学成绩的标准差 乙班10名同学成绩的标准差(填“>”,“<”);
(Ⅱ)从两班10名同学中各抽取一人,已知有人及格,求乙班同学不及格的概率;
(Ⅲ)从甲班10人中取一人,乙班10人中取两人,三人中及格人数记为X,
|
一选择题
1C 2B 3B 4B 5B 6B 7D 8D 9B 10D 11A 12A
二填空
13.70 14.试卷.files/image243.gif) 15.10 16.①④
15.10 16.①④
三、解答题
17.(本小题满分12分)。
(1)从已知条件试卷.files/image245.gif)
试卷.files/image247.gif) 故角A大小为60°;
故角A大小为60°;
(2)由余弦定理
试卷.files/image249.gif)
代入b+c=4得bc=3故△ABC面积为试卷.files/image251.gif)
18.(本题满分12分)
优秀
非优秀
总计
甲班
10
45
55
乙班
20
30
50
合计
30
75
105
解:(Ⅰ)
(Ⅱ)根据列联表中的数据,得到
试卷.files/image253.gif)
因此有95%的把握认为“成绩与班级有关系”。
(Ⅲ)设“抽到6或10号”为事件A,先后两次抛掷一枚均匀的骰子,出现的点数为(x,y)。
所有的基本事件有(1,1)、(1,2)、(1,3)、……、(6,6),共36个。
事件A包含的基本事件有:(1,5)、(2,4)、(3,3)、(4,2)、(5,1)(4,6)、(5,5)、(6、4),共8个
试卷.files/image255.gif)
19.(本小题满分12分)
(1)解:由该四棱锥的三视图可知,该四棱锥P-ABCD的底面是边长为1的正方形,
侧棱PC⊥底面ABCD,且PC=2.---------------------------------3分
∴试卷.files/image257.gif) ----------------------------6分
----------------------------6分
(2)不论点E在何位置,都有BD⊥AE---------------------------------------7分
证明如下:连结AC,∵ABCD是正方形
∴BD⊥AC∵PC⊥底面ABCD且试卷.files/image259.gif) 平面
平面试卷.files/image261.gif)
∴BD⊥PC-----------10分
又∵试卷.files/image263.gif) ∴BD⊥平面PAC
∴BD⊥平面PAC
∵不论点E在何位置,都有AE试卷.files/image265.gif) 平面PAC
平面PAC
∴不论点E在何位置,都有BD⊥AE----------------------------------------------12分
20.(本题满分12分)
解:试卷.files/image267.gif) ,
,
因为函数试卷.files/image193.gif) 在
在试卷.files/image166.gif) 处的切线斜率为-3,
处的切线斜率为-3,
所以试卷.files/image271.gif) ,即
,即试卷.files/image273.gif) ,①………………………2分
,①………………………2分
又试卷.files/image275.gif) 得
得试卷.files/image277.gif) .②………………………4分
.②………………………4分
(Ⅰ)函数试卷.files/image193.gif) 在
在试卷.files/image195.gif) 时有极值,
时有极值,
所以试卷.files/image280.gif) ,③………………………6分
,③………………………6分
联立①②③解方程组,得试卷.files/image282.gif) ,
,
所以试卷.files/image284.gif) .………………………8分
.………………………8分
(Ⅱ)因为函数试卷.files/image193.gif) 在区间
在区间试卷.files/image197.gif) 上单调递增,所以导函数
上单调递增,所以导函数试卷.files/image287.gif) 在
在
区间试卷.files/image197.gif) 上的值恒大于或等于零,
上的值恒大于或等于零,
则试卷.files/image289.gif) ………………………12分
………………………12分
解得试卷.files/image291.gif) ,
,
所以实数试卷.files/image199.gif) 的取值范围为
的取值范围为试卷.files/image294.gif) .………………………14分
.………………………14分
21.(本题满分12分)
解:(I)依题意,可知试卷.files/image296.gif) ,
,
∴试卷.files/image298.gif) ,解得
,解得试卷.files/image300.gif)
∴椭圆的方程为试卷.files/image302.gif)
(II)直线试卷.files/image213.gif) :
:试卷.files/image304.gif) 与⊙
与⊙试卷.files/image306.gif) 相切,则
相切,则试卷.files/image308.gif) ,即
,即试卷.files/image310.gif) ,
,
由试卷.files/image312.gif) ,得
,得试卷.files/image314.gif) ,
,
∵直线试卷.files/image213.gif) 与椭圆交于不同的两点
与椭圆交于不同的两点试卷.files/image217.gif) 设
设试卷.files/image316.gif)
∴试卷.files/image318.gif) ,
,
试卷.files/image320.gif)
试卷.files/image322.gif) ,
,
∴试卷.files/image324.gif)
∴试卷.files/image326.gif) ∴
∴试卷.files/image328.gif) ,
,
∴试卷.files/image330.gif)
试卷.files/image332.gif)
设试卷.files/image334.gif) ,则
,则试卷.files/image336.gif) ,
,
试卷.files/image338.gif)
∵试卷.files/image340.gif) 在
在试卷.files/image342.gif) 上单调递增∴
上单调递增∴试卷.files/image344.gif) .
.
22.(本题满分10分)
Ⅰ.选修4-1几何证明选讲
(I)∵DF是⊙O切线,切点为C,故∠DCA=∠ABC
Rt△ADC∽Rt△ACB
试卷.files/image346.gif)
试卷.files/image348.gif)
(II)BE是⊙O切线,C在图上
Rt△ABE中,由射定理得
试卷.files/image350.gif)
试卷.files/image352.gif)
又由(I)试卷.files/image354.gif)
试卷.files/image356.gif) ,
,试卷.files/image358.gif)
Ⅱ.选修4-2坐标系与参数方程
解:(I)曲线C的直角坐标方程为
试卷.files/image360.gif)
试卷.files/image362.gif)
试卷.files/image364.gif) 代入上式得
代入上式得试卷.files/image366.gif)
由线C极坐标方程试卷.files/image368.gif)
(II)由(I)⊙C圆心坐标试卷.files/image370.gif)
M点的直角坐标为试卷.files/image372.gif)
圆心到过M点直线距离的最大值为试卷.files/image374.gif) ,此时l被圆截得线段长量小.
,此时l被圆截得线段长量小.
试卷.files/image376.gif) 所求直线l方程
所求直线l方程
试卷.files/image378.gif)
Ⅲ.选修4-5不等式选讲
试卷.files/image380.gif)
试卷.files/image382.gif)
试卷.files/image384.gif)
试卷.files/image386.gif)
试卷.files/image388.gif)
试卷.files/image390.gif) .
.
当试卷.files/image392.gif) 时,不等式
时,不等式试卷.files/image394.gif)
不等式解为试卷.files/image396.gif)
当试卷.files/image398.gif) 时,不等式为
时,不等式为试卷.files/image400.gif)
不等式解为试卷.files/image402.gif)
当试卷.files/image404.gif) 时,
时,试卷.files/image406.gif)
试卷.files/image408.gif)
不等式解为试卷.files/image408.gif)
由上得出不等式解为试卷.files/image411.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com