
题目列表(包括答案和解析)
若抛物线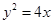 的焦点是
的焦点是 ,准线是
,准线是 ,则经过点
,则经过点 、
、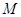 (4,4)且与
(4,4)且与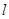 相切的圆共有
相切的圆共有
A. 个 B.
个 B.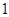 个
C.
个
C.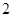 个
D.
个
D.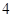 个
个
第Ⅱ卷
已知![]() 均为正数,
均为正数,![]() ,则
,则![]() 的最小值是 ( )
的最小值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷 (非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分,将答案填在题中的横线上。
给出定义:若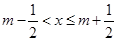 (其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m在此基础上给出下列关于函数
(其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m在此基础上给出下列关于函数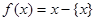 的四个命题:
的四个命题:
①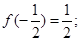 ②
②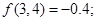
③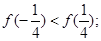 ④
④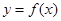 的定义域为R,值域是
的定义域为R,值域是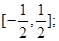
则其中真命题的序号是 ( )
A.①② B.①③ C.②④ D.③④
第Ⅱ卷
下列四个函数图象,只有一个是符合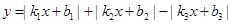 (其中
(其中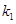 ,
,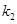 ,
,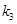 为正实数,
为正实数,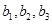 为非零实数)的图象,则根据你所判断的图象,
为非零实数)的图象,则根据你所判断的图象,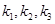 之间一定成立的关系是( )
之间一定成立的关系是( )
 |
A. 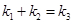 B.
B.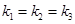 C.
C.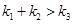 D.
D.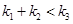
第Ⅱ卷
在等差数列 中,若
中,若 ,则
,则 的值为( )
的值为( )
A. 6 B. 8 C. 10 D. 16
第Ⅱ卷 (非选择题 共100分)
一、选择题(每小题5分,共60分)
BDACC ACDDB AA
二、填空题(每小题4分,共16分)
13. ; 14.
; 14. 15.―192 16.
15.―192 16.
三、解答题(共74分)
17.解:(I)由正弦定理 ,有
,有
代入 得
得
即



(Ⅱ)
由 得
得
所以,当 时,
时, 取得最小值为0
取得最小值为0
18.解:(I)由已知得
故
即
故数列 为等比数列,且
为等比数列,且
由当 时,
时,
所以
(Ⅱ)
所以


19.解:(I)从50名教师随机选出2名的方法为 =1225,选出2人使用教材版本相同的方法数
=1225,选出2人使用教材版本相同的方法数
故2人使用版本相同的概率为 。
。
(Ⅱ)
 的分布为
的分布为

0
1
2





20.解(I)由该四棱锥的三视图可知,该四棱锥 的底面是边长为1的正方形,
的底面是边长为1的正方形,
侧棱 底面
底面 ,且
,且 ,
,
(Ⅱ)不论点E在何位置,都有
证明:连结 是正方形,
是正方形,
 底面
底面 ,且
,且 平面
平面 ,
,

又 平面
平面
 不论点
不论点 在何位置,都有
在何位置,都有 平面
平面
 不论点E在何位置,都有
不论点E在何位置,都有 。
。
(Ⅲ)以 为坐标原点,
为坐标原点, 所在的直线为
所在的直线为 轴建立空间直角坐标系如图:
轴建立空间直角坐标系如图:
则 从而
从而



设平面 和平面
和平面 的法向量分别为
的法向量分别为
 ,
,
由法向量的性质可得:

令 则
则

设二面角 的平面角为
的平面角为 ,则
,则

 二面角
二面角 的大小为
的大小为 。
。
21.解:(1)由题意可知直线 的方程为
的方程为 ,
,
因为直线与圆 相切,所以
相切,所以 ,即
,即
从而
(2)设 ,则
,则 ,
,
又
(
①当 时,
时, ,解得
,解得 ,
,
此时椭圆方程为
②当 时,
时, ,解得
,解得 ,
,
当 ,故舍去
,故舍去
综上所述,椭圆的方程为
22.解:(I)依题意,知 的定义域为(0,+
的定义域为(0,+ )
)
当 时,
时,
令 ,解得
,解得 。
。
当 时,
时, ;当
;当 时,
时,
又 所以
所以 的极小值为2-2
的极小值为2-2 ,无极大值。
,无极大值。
(Ⅱ) ;
;
令 ,解得
,解得 。
。
(1)若 令
令 ,得
,得 令
令 ,得
,得
(2)若 ,
,
①当 时,
时, ,
,
令 ,得
,得 或
或 ;
;
令 ,得
,得
②当 时,
时,
③当 时,得
时,得 ,
,
令 ,得
,得 或
或
令 ,得
,得
综上所述,当 时,
时, 的递减区间为
的递减区间为 ,递增区间为
,递增区间为
当 时,
时, 的递减区间为
的递减区间为 ;递增区间为
;递增区间为
当 时,
时, 递减区间为
递减区间为
当 时,
时, 的递减区间为
的递减区间为 ,递增区间为
,递增区间为
(Ⅲ)当 时,
时,  ,
,
由 ,知
,知 时,
时,

依题意得: 对一切正整数成立
对一切正整数成立
令 ,则
,则 (当且仅当
(当且仅当 时取等号)
时取等号)
又 在区间
在区间 单调递增,得
单调递增,得 ,
,
故 又
又 为正整数,得
为正整数,得
当 时,存在
时,存在 ,对所有
,对所有 满足条件。
满足条件。
所以,正整数 的最大值为32。
的最大值为32。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com